



Dans une vitrine un peu sombre de la bibliothèque de l'Ecole, parmi d'autres objets scientifiques, se trouve une boîte en chêne, mystérieuse et discrète. Difficile de se douter, malgré l'inscription que porte son couvercle - Arithmomètre -, que l'on a sous les yeux un maillon essentiel de la grande épopée du calcul artificiel. Il s'agit en effet de la première machine arithmétique qui fût fabriquée à l'échelle industrielle. Son auteur, Thomas de Colmar, en prit le brevet en 1820. La machine de la collection date de la deuxième moitié du dix-neuvième siècle.
L'arithmomètre de Thomas hérite de siècles d'efforts obstinés pour délivrer les hommes de cette corvée fastidieuse qu'est le calcul numérique. C'est la somme de science et de technique contenue dans cet objet que je voudrais brièvement conter.
Ces "instruments" primitifs permettaient des opérations arithmétiques élémentaires comme l'addition et la soustraction. C'est ainsi qu'entre le Tigre et l'Euphrate, le berger sumérien comptabilisait son cheptel.
Au cours des millénaires ultérieurs les cailloux donnèrent lieu à la technique du calcul aux jetons. Probablement inventé par les Grecs, ce mode de calcul consiste à déplacer des jetons sur une grille appelée abaque, la valeur des jetons dépendant de leur place sur la grille. Perfectionné par l'apparition en Occident de la numération décimale, ce procédé fut universellement adopté par les comptables. Il ne fut définitivement abandonné qu'à la Révolution française.
Le premier véritable instrument de calcul, qui n'est pas encore une machine, est le boulier. En faisant coulisser les jetons dans des rainures, les Romains créèrent le premier instrument de ce type qui leur permit de surmonter l'incroyable complexité de leur numération. On sait le succès qu'eut le boulier au cours des siècles suivants puisqu'en Russie et en Extrême-Orient il est encore un concurrent sérieux de la calculette électronique.
Depuis l'antiquité grecque, des mécanismes compliqués étaient connus et appliqués à la production d'énergie, au levage et à la guerre, dans des machines que l'on appelle machines de force. Le Moyen Age les appliqua à l'horlogerie qui, avec l'orgue d'église, est sans doute le premier exemple de machine informationnelle. Mais aucun de ces artisans avisés qui les inventèrent et les perfectionnèrent, n'eut l'idée de construire une machine à compter. Pas même le génial Léonard de Vinci qui pourtant personnifie à lui seul les arts et les techniques de la Renaissance. Aucun n'osa franchir le pas de la mécanisation du calcul qui est considéré comme du domaine de la pensée.
Trois grands scientifiques et philosophes, Schickard, Pascal et Leibniz, osèrent le faire mais sans connaissances particulières en mécanique, ce qui leur valut de sérieux déboires. Comme nous le relate son ami Kepler, l'astronome Wilhelm Schickard construisit en 1623 la première machine arithmétique de tous les temps mais cette machine disparut peu de temps après dans un incendie dont les circonstances restent mystérieuses. En 1642, Biaise Pascal automatisa l'addition dans une machine - la pascaline - dont il nous reste actuellement neuf exemplaires. Ne trouvant pas d'horloger pour la réaliser, il dut en tailler lui-même les engrenages pour "animer le cuivre et donner de l'esprit à l'airain". Peu de temps après, en 1673, le philosophe et mathématicien Gottfried-Wilhelm Leibniz, dont on connaît les persévérantes recherches sur les mécanismes de la pensée, réussit, sans connaître les travaux de Pascal, à automatiser la multiplication grâce à des engrenages spéciaux dits cylindres de Leibniz et à l'invention du chariot mobile. Plus de deux siècles plus tard, ces deux pièces mécaniques restent les composants de base de la plupart des calculatrices. C'est le cas de notre arithmomètre de Thomas.
Le dix-huitième siècle, avec le marquis de Poleni, Braun, Leopold, lord Stanhope, Hahn et Müller, se contenta d'apporter quelques pièces uniques dignes des cabinets de curiosités scientifiques et des merveilleux automates androïdes qui le caractérisent si bien.
Les débuts de la révolution industrielle qui, en France, a débuté avec un décalage d'une cinquantaine d'années sur l'Angleterre, marquent un accroissement important du volume des calculs comptables. Par ailleurs la meilleure précision des moyens de la métrologie et des techniques de formage des métaux favorise la standardisation des pièces mécaniques. Ces deux raisons créent un terrain favorable à l'émergence d'une industrie des machines à calculer. Le pionnier mondial en est Thomas de Colmar, l'inventeur de notre arithmomètre N° 1398.
Thomas débute dans l'armée napoléonienne comme officier d'administration. A ce titre, il est chargé, pendant la campagne d'Espagne, d'assurer la subsistance du corps d'armée du maréchal Soult. Il y fait déjà la preuve de l'efficacité et de l'esprit d'initiative qui l'ont toujours distingué : au moment où les armées manquaient de tout, son corps d'armée était largement approvisionné ! C'est probablement à cette époque, que, surchargé de lourds calculs comptables, il conçoit l'idée de l'Arithmomètre. Il garde des liens étroits avec l'Espagne puisqu'il épouse, à Séville, la comtesse de Ampudia, née à Marbella, qui lui donnera une nombreuse famille.
Après la chute du Premier Empire, il réintègre la vie civile pour consacrer son activité à l'étude du fonctionnement des sociétés d'assurance, déjà prospères en Angleterre.
En 1819, à l'âge de trente-quatre ans, il fonde sa première compagnie d'assurance, la Compagnie du Phénix. Malgré ces occupations très absorbantes, il termine la mise au point de sa machine arithmétique en 1820. Cette première machine possède déjà l'élément essentiel des machines ultérieures : l'entraîneur à cylindres à dents de longueurs inégales (cylindres de Leibniz). Nul ne sait si Thomas eut connaissance de cette solution mécanique. La question n'a que peu d'importance. Maurice d'Ocagne (X 1880), professeur de géométrie à l'Ecole polytechnique de 1912 à 1936 et féru de calcul mécanique, constate "qu'en mettant en oeuvre, sous une forme nouvelle, certains organes antérieurement connus, combinés avec d'autres nouveaux, il est parvenu à établir une machine excellente au point de vue pratique, ce à quoi nul n'avait réussi avant lui, et cela n'est déjà pas un si mince mérite".
Thomas prend un brevet le 18 novembre 1820, "pour une machine ou appareil appelé arithmomètre, propre à suppléer à la mémoire dans toutes les opérations d'arithmétique". Cette invention lui vaut rapidement des distinctions prestigieuses : chevalier de la Légion d'honneur en 1821, puis promu officier par décret impérial en 1857, il reçoit la médaille d'or de la Société d'encouragement pour l'industrie nationale en 1851. A titre de récompense, de riches présents lui sont offerts par les plus hautes personnalités françaises et étrangères. En 1854, l'Académie des sciences donne son approbation à l'invention et l'astronome Le Verrier, directeur de l'Observatoire, adresse à Thomas une lettre de félicitations. On imagine difficilement aujourd'hui l'enthousiasme que souleva cette invention.
Parallèlement, Thomas poursuit son oeuvre de pionnier dans le domaine des assurances : en 1829, il crée une nouvelle société d'assurance, la Compagnie du Soleil, et en 1843, celle de l'Aigle. Devenu très fortuné, il acquiert successivement les châteaux de Maisons-Laffitte, ancien domaine seigneurial des barons de Longueil, le château de Champfleury, près de Poissy, et le château de Méré, ancien domaine de Poltrot, sire de Méré, près de Châtellerault.
Malgré son grand âge, sa robuste santé lui permet de continuer à diriger la Compagnie du Soleil. Il meurt à Paris, en 1870, à l'âge de quatre-vingt-cinq ans et est enterré au Père-Lachaise. C'est l'un de ses fils, Louis-Nicolas-André, duc de Bojano par son mariage, qui lui succède à la tête de la Compagnie du Soleil.
La machine proprement dite est en bronze et en acier. Sa face supérieure rassemble toutes les commandes et tous les afficheurs. Elle comporte une platine fixe et un chariot mobile.
La platine fixe porte des rainures graduées dans lesquelles coulissent des curseurs destinés à inscrire le nombre sur lequel on veut opérer. Sur la droite, une manivelle escamotable, à poignée d'ivoire, permet d'actionner l'entraîneur. Elle ne peut tourner que dans le sens des aiguilles d'une montre. Sur la gauche, se trouve un levier à deux positions pour l'addition (multiplication) et la soustraction (division). Une petite plaque en verre dépoli permet d'inscrire au crayon les résultats intermédiaires des calculs. Elle dissimule un petit casier de rangement où l'on trouve en particulier de petites chevilles d'ivoire, destinées à marquer les virgules et les ordres décimaux.

Arithmomètre de Thomas de Colmar No 1398 (vers 1870)
La machine est contenue dans une boîte en chêne. La platine en bronze se compose d'une partie
fixe et d'un chariot mobile. Sur la partie fixe, on distingue, de droite à gauche : la manivel le
d'entraînement, repliable, les curseurs d'inscription, le levier addition/soustraction et la
plaque en verre dépoli pour l'inscription des résultats intermédiaires. Sur le chariot, on distingue
les lucarnes du totalisateur (16 chiffres) et du compteur (9 chiffres), ainsi que les boutons
moletés des effaceurs, qui servent aussi à saisir le chariot pour le faire avancer.
© Ecole
polytechnique/Inventaire général. M. Lebée.

Mécanisme de l'Arithmomètre
Une fois extraite de sa boîte, le mécanisme de la machine apparaît: on remarque les cylindres cannelés de
Leibniz, à dents de longueurs inégales, qui forment l'entraîneur. La qualité de finition et la robustesse
des pièces, taillés dans l'acier et le bronze, sont remarquables.
Le principe est le suivant : le curseur d'inscription entraîne une fourchette qui déplace un pignon parallèlement à la génératrice du cylindre entraîneur. Suivant la position du curseur, le pignon engrène sur un nombre variable de dents. Comme il coulisse sur un axe de section carrée, il entraîne le totalisateur, par l'intermédiaire de roues d'angle. A chaque rotation complète de la manivelle, le cylindre entraîneur accomplit une révolution et fait avancer le totalisateur d'une quantité égale au chiffre inscrit au curseur correspondant.
Le mécanisme de report de retenues est assez complexe, mais de fonctionnement très sûr. Plusieurs mécanismes de report furent expérimentés antérieurement et durent être abandonnés faute de fiabilité.
Afin que les reports ne s'effectuent pas simultanément, ce qui pourrait entraîner le blocage de la machine, le montage des cylindres cannelés est décalé, chacun étant en retard d'un vingtième de tour sur le précédent dans son mouvement de rotation. Grâce à cette disposition, si tous les cadrans du totalisateur affichent le chiffre 9, l'addition d'une unité au nombre ainsi formé, provoque l'apparition successive de zéros dans les lucarnes, de la droite vers la gauche, sans que l'effort à fournir sur la manivelle soit à chaque instant supérieur à celui qu'il faut développer pour un report unique. On trouvait déjà un report en cascade de ce type sur la machine de Pascal.
Comme le fonctionnement de ce reporteur n'est pas réversible, une pignonnerie à doubles roues d'angle permet d'inverser le sens de rotation des disques totalisateurs pour la soustraction et la division.
Pour éviter les erreurs qui pourraient être provoquées par l'inertie des pièces en mouvement rapide, les axes des roues totalisatrices portent des cames en forme de croix de Malte qui ne les libèrent qu'au moment où ils doivent entrer en mouvement.
Le totalisateur et le compteur sont munis d'un dispositif ingénieux de remise à zéro que l'on appelle effaceur. Les deux boutons moletés situés aux extrémités du chariot actionnent une crémaillère, placée sous la platine. Cette crémaillère vient engrener avec des roues dentées montées sur les mêmes axes que les cadrans afficheurs. Chaque roue possède 10 dents mais celle qui correspond au 0 a été enlevée. La crémaillère est donc en prise sur la roue jusqu'à l'emplacement de la dent manquante; la roue s'arrête alors sur le zéro.
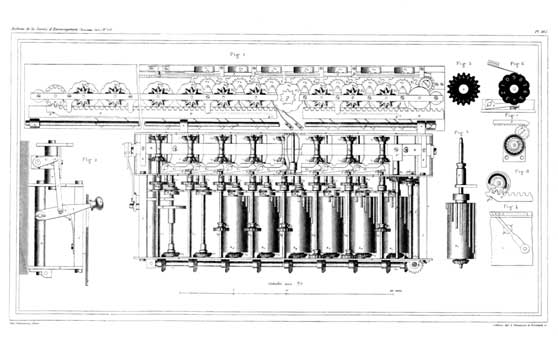
Mécanisme de l'Arithmomètre
Sur cette superbe planche, on découvre de bas en haut : les cylindres cannelés de Leibniz avec leur arbre d'entraînement, mû par la manivelle, les leviers horizontaux du reporteur, les pignons coniques jumelés permettant l'inversion de marche et le chariot avec les pignons et les disques du totalisateur et du compteur. Sur la droite de la planche sont figurés deux disques chiffrés, du compteur et du totalisateur, un cylindre de Leibniz avec son ergot de report de retenue et les dispositifs d'entraînement des crémaillères d'effacement. (planche du Bulletin de la Société d'encouragement pour l'industrie nationale, sept-oct. 1920, p. 712 et 713).
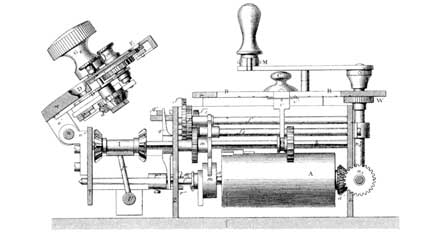
Principe de l'entraîneur de l'Arithmomètre de Thomas
L'entraîneur utilise le principe des cylindres cannelés de Leibniz. L'un de ces cylindres , entraîné par la manivelle, est représenté en A. Il porte une denture en forme de nervures de différentes longueurs (9 au total). Le curseur d'inscription C, visible en haut, permet, grâce à une fourchette, de déplacer un pignon coulissant B sur un axe de section carrée qui actionne la roue du totalisateur. Le pignon engrène avec un nombre de dents égal au chiffre inscrit. A chaque tour de manivelle, ce chiffre est ajouté au contenu du totalisateur. On notera l'ergot de report fixé au cylindre et les pignons d'inversion de marche I.Dictionnaire Lami, p. 272, fig 139.
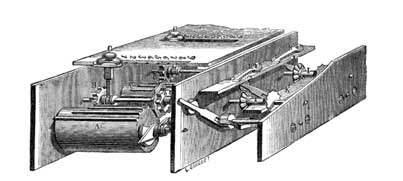
Coupe du mécanisme de l'Arithmomètre
Sur cette vue en coupe du mécanisme, le chariot est relevé. On distingue très clairement les cylindres de Leibniz avec leur mécanisme d'entraînement et la manivelle, un curseur d'inscription et son pignon, le mécanisme d'inversion à doubles pignons d'angle, et le reporteur. (Bulletin de la Société d'encouragement, sept. oct. 1920, p. 697 fig. 2)
Un curseur supplémentaire, à gauche, affiche les chiffres du multiplicateur, au fur et à mesure du déroulement de l'opération.
Le mouvement de l'entraîneur est assuré, non par une manivelle, mais par un ruban qui s'enroule sur un barillet à ressort. Les opérations sont effectuées en tirant le ruban de la main gauche, sans se préoccuper du nombre de tours de l'entraîneur. Ensuite, le ruban revient automatiquement à sa place sous l'action du ressort. On se demande pourquoi une conception aussi simple et aussi ergonomique n'a pas été maintenue dans les modèles ultérieurs.
Pendant plus de soixante ans, de nombreux perfectionnements ont été apportés à la machine, souvent par des collaborateurs anonymes, quelquefois de simples ouvriers, que Thomas, bien qu'absorbé par ses autres occupations, trouvait toujours le temps d'encourager. Son fils, Thomas de Bojano, contribua activement, lui aussi, au perfectionnement de la machine, ainsi que MM. Darras et Payen qui eurent la charge de sa fabrication industrielle.
Les principales améliorations ont porté sur :
Pendant un demi-siècle, la machine fut seule sur le marché. Pendant un autre demi-siècle, jusqu'aux années 1920, elle soutint la concurrence d'autres modèles, beaucoup plus récents, comme les machines de Odhner et le Comptometer de Felt.
Toutefois, par suite des imperfections des premiers modèles et de l'inexistence du marché, ses débuts furent lents. De 1821 à 1865, c'est à dire en plus de quarante ans, 500 machines seulement furent vendues. En revanche, de 1865 à 1878, la vente s'éleva à plus de 1000 machines, dont environ le tiers de machines de 6 chiffres, les deux tiers de machines de 8 chiffres et 10% de machines de 10 chiffres. Une part importante de cette production (60%) était destinée à l'étranger, où par ailleurs de nombreuses copies étaient fabriquées, notamment en Allemagne et en Angleterre.
Ce succès éclatant est dû, non seulement aux qualités intrinsèques de la machine, mais aussi à sa fiabilité exceptionnelle qui fait que l'on peut l'utiliser journellement pendant dix ans, sans qu'il soit besoin d'intervenir pour la réparer.
En France et à l'étranger, les principaux utilisateurs étaient les administrations, les grandes entreprises, les banques, les laboratoires, les compagnies d'assurance et les grands magasins : Caisse des dépôts et consignations, magasins du Louvre, Compagnie des petites voitures, direction de l'artillerie au Ministère de la Guerre, Ministère de la Marine, les observatoires de Paris et de Cambridge, l'établissement du Creusot, Ecole polytechnique, Ecole des ponts et chaussées, Ecoles polytechniques et des arts et métiers d'Allemagne, de Prusse, de Suisse et de Russie, Compagnies de chemins de fer, etc.
Les utilisateurs sont unanimes pour reconnaître les gains de productivité obtenus grâce à l'arithmomètre. L'administration du chemin de fer du Nord constate que "deux employés, l'un manipulant, l'autre transcrivant les résultats, peuvent faire la besogne de six".
Un opérateur entraîné exécute une multiplication de 8 chiffres par 8 chiffres en 18 secondes, une division de 16 chiffres par 8 chiffres en 24 secondes et l'extraction d'une racine carrée de 16 chiffres, avec la preuve, en 75 secondes... En revanche, l'addition et la soustraction sont relativement lentes, car elles nécessitent chaque fois l'inscription d'un nouveau nombre. Dans ces opérations, la machine n'est guère plus rapide qu'un calculateur entraîné. Il faudra attendre l'introduction du clavier à touches, sur des machines dérivées de l'Arithmomètre, pour enregistrer un progrès notable.
Notre arithmomètre est-il pour autant l'ancêtre du micro-ordinateur ? Certainement pas. L'ordinateur est une machine de traitement de l'information pour laquelle les opérations arithmétiques ne sont que des tâches subalternes. La variété des tâches qu'il peut traiter est illimitée. Sa puissance provient de son universalité. Chaque nouveau logiciel en fait une machine nouvelle. Les principes fondateurs de l'ordinateur sont à rechercher dans les premières réalisations de machines logiques comme le Demonstrator de Lord Stanhope (1770) et surtout dans la machine analytique de Babbage (1834) qui, pour la première fois, mettait en application les concepts de programmation et de traitement conditionnel. Malheureusement, comme on sait, les limitations propres aux techniques mécaniques empêchèrent Babbage de mener à bien son projet.
Les machines arithmétiques, dont l'arithmomètre de Thomas, n'en restent pas moins les premiers exemples de la mécanisation de la pensée, qui a toujours fasciné et inquiété les hommes. Pascal en était déjà conscient quand il rassurait ses contemporains en affirmant que sa machine n'avait pas de "volonté comme les animaux". Maintenant qu'une machine a battu le champion du monde des échecs, nous nous rassurons, à l'instar de Pascal, en invoquant la lourdeur et le manque d'"intelligence" des algorithmes mis en jeu, mais nous risquons d'être surpris par ce que nous réserve l'avenir.
Anderson (A.R.). Pensée et machine. Champ Vallon, 1983.
Breton (P.). Histoire de l'informatique. Paris : Editions de la Découverte, 1987.
Cohen (J.). Les robots humains dans le mythe et dans la science. Paris : Vrin, 1968.
Couffignal (L.). Les machines à penser. Paris : Editions de Minuit, 1952.
Daumas (M.). Histoire générale des techniques. Paris : PUF, (1962-1979).
Ekeland (I.). Le calcul, l'imprévu. Paris : Le Seuil, 1984.
Gille (B.). Les mécaniciens grecs. Paris : Le Seuil, 1980.
Ifrah (G.). Histoire universelle des chiffres. Paris : Laffont, 1994.
Jacob (L.). Le calcul mécanique. Paris : Doin, 1911.
Kradolfer (P.). Einige Rosinen aus der Entwicklung der Rechenmaschinen. Suisse : Verlag
Sauer länder AG, 1988.
La Mettrie (réimpression). L'homme-machine. Paris : Denoël-Gontier, 1981.
Levy (P.). La machine univers. Paris : Editions de la Découverte, 1987.
Ligonnière (R.). Préhistoire et histoire des ordinateurs. Paris : Laffont, 1987.
Marguin (J.). Catalogue de l'exposition "De la machine à calculer de Pascal à l'ordinateur". Musée national des techniques. Paris : CNAM, 1990.
Marguin (J.). Le reporteur et la naissance du calcul mécanique. Paris : La Revue CNAM, 1993.
Marguin (J.). Histoire des instruments et machines à calculer. Hermann, Paris : 1994
Marguin (J.). Une histoire du calcul artificiel et de ses concepts. Paris : Sciences, AFAS, 1997.
Martin (E.). Die Rechenmaschinen und ihre Entwicklungsgeschichte. Hambourg : Hans Burghagen Verlag, 1925.
Molk (J.). Encyclopédie des sciences mathématiques . T.l, Vol. 4. Paris : Gauthier-Villars, 1906. Réédition Paris : J. Gabay, 1993.
Moreau (R.). Ainsi naquit l'informatique. Paris : Bordas, 1984.
D'Ocagne (M.). Le calcul simplifié. Paris : Gauthier-Villars, 1905.
Russo (F.). Introduction à l'histoire des techniques. Paris : Albert Blanchard, 1986.
Taton (R.) et Flad (J.P.). Le calcul mécanique. Paris : PUF, 1963.