



La méthode de Cholesky , bien connue de tous ceux qui font des calculs numériques sur ordinateur, sert à résoudre certains systèmes d'équations linéaires. On la trouve présentée dans presque tous les livres d'analyse numérique.
Jusqu'à ces derniers temps, elle n'était connue que de seconde main puisque Cholesky n'avait jamais rien publié lui-même sur ce sujet. Mais une personne de sa famille, M. Gross-Cholesky, vient de déposer les documents qu'il possédait, aux Archives de l'Ecole Polytechnique où Cholesky fut élève. Ils forment maintenant le Fonds A. Cholesky. Parmi ces documents se trouve un manuscrit, de la main même de Cholesky, où il expose sa méthode. C'est donc un document scientifique de première importance. D'autres documents intéressants ont également été retrouvés; ils sont décrits dans le présent bulletin.
La biographie de Cholesky présentée ici tient compte des archives militaires qui ont été ouvertes au public en octobre 1995 [1], des documents contenus dans le Fonds A. Cholesky de l'École Polytechnique, et de souvenirs familiaux. Certaines indications ont été empruntées à [5]. Une première biographie de Cholesky a été publiée dans [12].
André Louis Cholesky naquit le 15 octobre 1875, à une heure du soir comme l'indique son acte de naissance, à Montguyon, petite commune de l'arrondissement de Jonzac (Charente Maritime) à 35 km environ au nord-est de Bordeaux, qui compte actuellement de l'ordre de 1700 habitants et où l'on traite les argiles blanches et fabrique des parquets et des lambris. Il était le fils d'André Cholesky, maître d'hôtel, né le 9 octobre 1842 à Montguyon (lui-même fils de Louis Cholesky, 28 ans, cordonnier, et d'Anne Moreau, âgée de 32 ans) et de Marie Garnier, 27 ans. Dans son livret matricule d'officier, il est fait mention du surnom de René (c'est d'ailleurs ce prénom qui est inscrit sur sa tombe). André avait de nombreux frères et sœurs. La famille, des gentilshommes dont le blason était Cholewa, avait émigré en France à l'époque napoléonienne. C'étaient de bons patriotes dont le nom, à l'origine, s'écrivait Cholewski. C'est sans doute pour cela que, sur certains documents en sa possession, Cholesky avait lui-même orthographié son nom Choleski.
Avec Google, le patronyme Cholesky fournit 78200 réponses, Choleski en donne 5880 et Cholewsky 90 [rédigé en 2005 ; ces nombres étaient en octobre 2007 respectivement : 727000, 5800 et 88].
On semble ne rien savoir de son enfance qu'il passa vraisemblablement à Montguyon. Il fut élève au lycée de Saint-Jean-D'Angély (à l'intérieur du Lycée Audouin-Dubreuil son nom apparaît sur la plaque commémorative des anciens élèves et professeurs Morts pour la France).
Il obtint la première partie de son baccalauréat à Bordeaux le 14 novembre 1892 et sa seconde partie, avec la mention assez bien, le 24 juillet 1893, toujours à Bordeaux. Le 15 octobre 1895, il entre à l'École Polytechnique, 87ème sur 223 et signe un engagement de 3 ans dans l'armée à la mairie du 5ème arrondissement de Paris. Sa fiche signalétique le décrit comme ayant les cheveux et les sourcils châtain clair, le front haut, le nez long, les yeux châtains, la bouche moyenne, le menton rond et le visage ovale. Il mesure 1m75. Le commandant de l'École est alors le Général Louis Joseph Nicolas André (Nuits, Côte d'Or, 29 mars 1838 - Dijon, 18 mars 1913) et le Directeur des Études s'appelle Ernest Jules Pierre Mercadier (Montauban, 4 janvier 1838 - Paris, 27 juillet 1911). Ses professeurs sont Camille Marie Ennemond Jordan (Lyon, 5 janvier 1838 - Paris, 21 Janvier 1922) et Marie Georges Humbert (Paris, 7 janvier 1859 - Paris, 22 janvier 1921) pour l'analyse mathématique, Jacques Rose Ferdinand Emile Sarrau (Perpignan, 24 juin 1837 - Paris, 10 mai 1904) et Henri Charles Victor Jacob Léauté (Bazile, 26 avril 1847 - Paris, 5 novembre 1916) pour la mécanique, Paul Emile Haag (Paris, 10 janvier 1843 -26 avril 1911) pour le géométrie, Marie Alfred Cornu (Orléans, 6 mars 1841 - La Chausonnerie, près de Romorantin, 12 avril 1902) et Henri Antoine Becquerel (Paris, 15 décembre 1852 - Le Croisic, 25 août 1908) pour la physique, Henri Gal (né à Marseille, le 15 juin 1839) pour la chimie, Dartein pour l'architecture, Auguste George Gabriel Duruy (né à Paris, le 10 mars 1853) pour l'histoire et la littérature et Jean-Baptiste Claude Eugène Guillaume (Montbard, Côte d'Or, 4 juillet 1822 - Rome, 1905) pour le dessin [14]. Enfin, il ne faut pas oublier Octave Pierre Jean Callandreau (Angoulême, 18 septembre 1852 - Paris, 13 février 1904) dont les cours d'astronomie et de géodésie durent avoir une grande influence sur l'orientation de Cholesky. Le Major d'entrée et de sortie est un certain Jules Louis Crussard (Neufchâteau, Vosges, 10 juin 1876 - 2 janvier 1959). En 1896, Cholesky passe de deuxième en première division 56ème sur 222 et sort de l'École en 1897, 38ème sur 222. Il est admis dans l'Artillerie 4ème sur 92. Sa conduite et sa tenue sont qualifiées de très bonnes et son instruction militaire d'assez bonne.
Il est Sous-Lieutenant, élève à l'École d'Application de l'Artillerie et du Génie de Fontainebleau à partir du 1er octobre 1897. Il en sort en 1899, 5ème sur 86. Il y suit des cours d'artillerie, de fortification permanente, de construction, d'art militaire, de mécanique, de sciences appliquées, d'hippiatrique ( ? ), d'histoire militaire et de géographie de la France et de ses Colonies. Les cours d'artillerie militaire comprenaient 55 journées d'application avec 5 dessins et 9 mémoires et portaient sur la balistique, l'application aux questions de tir et l'étude des tables de tir, les levés de bâtiments et d'usines, des projets de machines et des coupes géologiques de terrain. Il y avait également un cours de topographie qui fut donné, avant l'arrivée de Cholesky, par le Lieutenant-Colonel Charles-Moyse Goulier (Richelieu, 1818 - Paris, 1891), X 1836, l'inventeur, entre autres, de l'alidade nivellatrice, de l'alidade holométrique et de la règle à éclimètre, instruments qui seront décrits par Cholesky dans ses livres. Les exercices topographiques exigeaient de la part des élèves de sérieuses qualités de dessinateur et, à ce propos, Goulier signale qu'ils sont d'une inhabileté extrême. Enfin, à partir de 1897, les moniteurs de gymnastique donnèrent des leçons facultatives de bicyclette [9].

Le 1er octobre 1899, Cholesky est nommé Lieutenant en second au 22ème Régiment d'Artillerie. Du 17 janvier 1902 au 27 juin, il effectue une mission en Tunisie, puis une autre du 21 novembre 1902 au 1er mai 1903. Du 31 décembre 1903 au 6 juin 1904, on le retrouve en Algérie. Le 24 juin 1905 il est affecté au Service Géographique de l'État-Major de l'Armée. Il s'y fera immédiatement remarquer (voir la section 1.4 ainsi que [5]) par une vive intelligence, une grande facilité pour les travaux mathématiques, des idées originales et parfois même paradoxales, mais toujours empreintes d'une grande élévation de sentiments, et qu'il soutenait avec beaucoup de chaleur.
À cette époque, suite à la révision de la méridienne de Paris, une nouvelle triangulation cadastrale de la France venait d'être décidée ainsi que la mesure de la méridienne de Lyon. Ces missions avaient été confiées à la section de Géodésie ainsi que l'établissement de la carte de l'Algérie et le nivellement géométrique précis de ce pays. Le problème de la compensation des réseaux (corrections à apporter aux angles mesurés) préoccupait bon nombre d'officiers du Service Géographique désireux de trouver une méthode simple, rapide et précise. D'après la notice nécrologique rédigée par le Commandant Benoît [5], c'est à cette occasion que Cholesky imagina sa méthode pour résoudre les équations de condition par la méthode des moindres carrés. Ce procédé de calcul très ingénieux rendit aussitôt de grands services.
Citons le rapport [2]
En 1905, ces deux géodésiens avaient fait les observations de la partie Est du Parallèle Moyen et du rattachement de ce parallèle à la Méridienne de Lyon. Tous deux étant partis, à la fin de la même année, rejoindre la Mission géodesique française de l'Equateur, les observations de la Méridienne de Lyon furent confiées, en mai 1906, au capitaine Lamotte, secondé par le capitaine Benoît.
Le programme de 1906 consistait à achever la liaison de la méridienne au Parallèle de Paris, et à poursuivre les observations en s'étendant de ce parallèle vers le Sud.
En 1904, le capitaine Durand avait fait complètement les observations des stations de Vaudémont, Hautmont et Haudompré avec le poids 24; mais les signaux de Croix-Marguerite et de Champfleury n'avaient pas été construits.
En 1906, il fallait donc construire deux derniers signaux, ainsi que Chailluz, La Serre, Mont-Poupet et Pierre; observer en Moncel et Essey pour compléter le rattachement du Parallèle de Paris à la Méridienne de Lyon; reprendre les observations en Hautmont et Haudompré; et continuer au Sud par les stations de Croix-Marguerite, Champfleury, Chailluz et La Serre. Ce programme a été exécuté de point en point.
La partie de la Méridienne de Lyon comprise entre le parallèle de Paris et le parallèle moyen avait été reconnue en 1904 : au Nord et au Centre, par le capitaine Durand; au Sud, par le commandant de Fonlongue. Les emplacements de tous les signaux avaient été parfaitement définis, et la hauteur à donner à chacun d'eux exactement déterminée à l'aide de l'échelle de reconnaissance.
Cholesky prendra part à ces campagnes de mesure dans la vallée du Rhône, dans le Dauphiné, dans l'Isère et dans les Cévennes, à Montellier, près du Mont Aigoual (juillet et septembre 1905) et à la Charpenne. Il est important de noter la présence du Capitaine Benoît, sans doute celui-là même qui écrira la notice nécrologique de Cholesky [5] et publiera sa méthode en 1924 [10].
Le 26 septembre 1905, Cholesky passe Lieutenant en premier. Il épouse, le vendredi 10 mai 1907 à la mairie de La Roche-Chalais (Dordogne), par autorisation ministérielle du 22 avril 1907, sa cousine germaine Anne Henriette Brunet, née le 27 juin 1882. Elle est la fille de François Brunet, âgé de 52 ans, propriétaire agriculteur, et de Anne Garnier, sa tante. À cette époque, il habite au 33bis rue Rosa Bonheur, Paris 15ème. Ils auront deux fils, dont un posthume, et deux filles: René (né en 1908), Françoise (née en 1909), Hélène (née de 1911) et André (né en 1919), tous décédés. Actuellement plus aucun descendant ne porte son nom.
Les mesures de la méridienne de Lyon continuent. Les observations commencent à Pierre-en-Besse (10 juin au 7 juillet 1907). D'abord retardées par la pluie et la brume, elles sont ensuite favorisées par un temps exceptionnellement beau. Il en est de même au mont Poupet (8 au 25 juillet 1907) à cause de brumes solaires. Des signaux sont construits à La Mouillère (en deux jours), à La Chalentinne et à Nivigne (en trois semaines, jusqu'à fin septembre, par suite d'une longue période de brumes très intenses). D'autres signaux sont élevés au Crêt de la Neige, au Grand Colombier et au Granier en moins d'un mois. En 1907, la portion de la chaîne allant du parallèle moyen du côté La Serre-Chailluz au côté Montellier-Grand Colombier est terminée. On retrouve certains de ces noms dans les carnets de Cholesky.
Cholesky effectue une mission en Crète, alors occupée par les troupes internationales, du 7 novembre 1907 au 25 juin 1908. À la suite d'une proposition du Colonel Lubanski, Commandant supérieur des troupes françaises en Crète et lui-même ancien géodésien, et d'une reconnaissance rapide effectuée en mars-avril 1906 par le Lieutenant-Colonel Robert Joseph Emile Bourgeois (Sainte Marie aux Mines, 21 février 1857 - 10 novembre 1945, X 1876, qui deviendra Général et sera élu à l'Académie des Sciences, Section Géographie et Navigation, le 18 juin 1916) qui commandait la section de géodésie, il avait été décidé d'entreprendre la triangulation des secteurs français et britannique de l'île (départements de San Nicolo et de Candie) ainsi que le levé topographique du secteur français. Trois officiers, dont Cholesky et le Commandant Lallemand, effectuent pendant trois mois les travaux préliminaires : mesure d'une base de 8 km de longueur dans la plaine de Kavousi et détermination d'une latitude et d'un azimut astronomiques au terme sud. Puis Cholesky reste seul trois mois de plus pour exécuter la triangulation des secteurs français et anglais. Les reconnaissances de terrain et la construction des signaux se poursuivirent en plein hiver. La Crète, large de 57 kilomètres au maximum et longue de 250, culmine à plus de 2400 mètres. À la fin mai, il était encore nécessaire, sur les hauteurs de Lassithi, de faire fondre la neige pour obtenir l'eau nécessaire au détachement. On conçoit donc la difficulté de la tâche qui se termina vers la mi-juin 1908. Malheureusement les circonstances politiques ne permirent pas de faire ensuite les relevés topographiques. [Le commandant Nicolas Arthur Lallemand (1859-1946 ; X 1877) était le frère de Charles Jean-Pierre Lallemand (1857-1938 ; X 1874), directeur du service du nivellement de la France, qui devint membre de l'Académie des sciences en 1910].

Le 25 mars 1909, Cholesky est nommé Capitaine en second au 27ème Régiment d'Artillerie et maintenu au Service Géographique. Le 28 août 1909, il est rayé des contrôles du Service Géographique et rejoint, le 14 septembre par décision ministérielle, le 13ème Régiment d'Artillerie afin d'y effectuer son temps légal de deux ans comme commandant de la 13ème batterie qui venait d'être créée. C'est à cette époque qu'il rédige le manuscrit sur sa méthode de résolution des systèmes d'équations linéaires, la fameuse méthode de Cholesky. Ce manuscrit est conservé dans le Fonds A. Cholesky de l'École Polytechnique.
Le 24 septembre 1911, il est affecté à l'état major particulier de l'artillerie et, le 13 octobre de la même année, au Service Géographique de l'armée dirigé par le Général Bourgeois qui avait comme adjoint le Capitaine Chicoyneau de Lavalette du Coetlosquet. La direction du nivellement en Algérie et en Tunisie lui est confiée. Le chef de la Section de Géodésie est le Lieutenant Colonel Lallemand, lui-même brillant géodésien. Du 27 octobre 1911 au 24 avril 1912, il effectue des travaux géodésiques en Algérie avec un séjour de 4 jours au Sahara (26-30 mars 1912) dans l'Oasis du Rhir. Le 8 octobre 1912, il est de nouveau désigné pour prendre part à la campagne 1912-1913 des travaux de nivellement en Algérie et en Tunisie. Il devra être rendu à Marseille pour s'y embarquer le 25 octobre 1912 à 13h à destination d'Alger. Il a droit à une indemnité de 10 F. par jour pour travaux géodésiques et à 5 F. pour indemnité de montagne. Il est autorisé à emmener son soldat d'ordonnance mais pas son cheval. Il devra rentrer à Paris à l'issue de sa mission. Il poursuivit donc, avec son ardeur habituelle, les travaux de triangulation en vue de l'établissement de cartes et ceux de nivellement de précision en Algérie et en Tunisie entre octobre 1912 et le 17 avril 1913. En Algérie, ces travaux avaient pour but la construction d'une ligne de chemin de fer entre Orléansville, Vialar et Trumelet afin de relier le plateau agricole du Sersou à la vallée du Cheliff. Des difficultés considérables furent rencontrées à cause du terrain accidenté et de la rigueur du climat du massif de l'Ouarsenis. Un tronçon de la route entre Biskra et Touggourt fut également nivelé. En Tunisie, le nivellement de précision des routes et des voies ferrées de la région de Tunis fut mené à bien. Le réseau primordial tunisien fut terminé sur le terrain pendant l'hiver 1913-1914, les calculs immédiatement revus, remis en ordre, le réseau arrêté et compensé [3]. Au mois de mai 1912, Cholesky avait reçu l'ordre d'étudier un procédé de nivellement permettant de travailler plus vite qu'en Algérie et en Tunisie tout en conservant une précision suffisante afin que les résultats puissent être immédiatement utilisables dans l'étude des chemins de fer et aussi, éventuellement, dans le cadre d'ensemble des lignes à niveler ultérieurement au Maroc. La méthode et les conditions générales du travail furent d'abord étudiées au bureau puis essayées sur le terrain au polygone de Vincennes par quatre militaires mis à la disposition de Cholesky. Ceux-ci partirent pour Casablanca au début de juillet 1912 et opérèrent au Maroc jusqu'en janvier 1913. Le livret matricule d'officier de Cholesky fait état vers cette époque, mais sans précision de date, de blessures.

Le 25 mai 1913, Cholesky est placé hors cadre, à la disposition du Ministre des Affaires Étrangères, et est nommé chef du service topographique de la Régence de Tunis. Il y reste jusqu'au 2 août 1914, date de la mobilisation, où il rejoint le 7ème groupe d'artillerie à Bizerte. Le 15 septembre il s'embarque à Bizerte pour rejoindre le dépôt du 16ème Régiment d'Artillerie basé à Issoire. Il débarque à Marseille le 17.
À partir de décembre 1909 (et peut-être avant) jusqu'à janvier 1914 au moins, Cholesky participe à l'enseignement par correspondance de l'Ecole Spéciale des Travaux Publics, du Bâtiment et de l'Industrie fondée en 1891 par Léon Eyrolles. Cette école comportait cent dix professeurs et sept mille élèves, internes, externes ou correspondants, dans tous les pays du monde. Cholesky doit corriger des devoirs envoyés par les élèves et surtout rédiger des cours. On possède plusieurs lettres du Directeur Adjoint les lui réclamant avec insistance. Il est chargé d'un cours de Topographie Générale et d'un cours de Calcul Graphique des Contenances. En janvier 1914, il reçoit même une lettre lui demandant de préparer un cours de Notions de Cosmographie et d'Astronomie de Position. On trouve dans les papiers qu'il a laissés des manuscrits correspondant à ces cours, ainsi que des exercices qu'il avait préparés.
Le 24 septembre 1914, Cholesky est nommé commandant de la 9ème batterie du 23ème Régiment d'Artillerie. Le 27 septembre, il est désigné pour remplacer le commandant du 3ème groupe qui vient d'être évacué. Il y fait fonction de Chef d'Escadron jusqu'au 18 octobre. Par suite de l'arrivée du Commandant Girard, il retourne au commandement de sa batterie.
Au début de la guerre, les cartes d'État Major françaises au l/80000ème utilisaient la projection de Bonne. L'artillerie, qui tirait jusque là à vue, fut amenée à pointer des objectifs invisibles définis par leur position sur une carte. L'expression de plan directeur provient du fait qu'il était utilisé pour diriger le tir de batteries. Il fallait perfectionner la préparation des tirs en s'appuyant sur des cartes plus précises où le relief devait être représenté. Il était également indispensable d'y faire figurer les positions ennemies. On ne pouvait aller les lever directement sur le terrain. On fit donc appel à la photographie aérienne alors débutante. Les avions volent bas, sont instables et prennent des photographies obliques qu'il faut ramener à l'horizontale. Cholesky participa à tous ces travaux.
Les Groupes de Canevas de Tir furent créés vers la fin de 1914. Ils devaient fournir des cartes quadrillées, primordiales pour les calculs de pointage des artilleurs qui tiraient sur des objectifs invisibles et devaient faire face à la prolifération des systèmes locaux de coordonnées. C'est pourquoi, le Général Directeur du Service Géographique de l'Armée demanda, par une note du 10 avril 1915, leur avis à ces groupes sur le choix d'une projection unique pour tout le front. Fut retenue la proposition du Chef de Bataillon Lavalette-Coëtlosquet, qui commandait le groupe de canevas de tir de la 1ère Armée. Elle consistait à adopter la projection conforme proposée par le mathématicien Johann Heinrich Lambert (Mulhouse, Suisse, 26 août 1728 - Berlin, 25 septembre 1777) en 1772 [27]. Cette méthode de projection permettait de représenter la surface sphérique de la Terre en conservant les angles, de ne pas déformer le terrain, de respecter les dimensions relatives, de conserver l'échelle des distances et les alignements afin de pouvoir calculer les coordonnées. La décision du 18 juin 1915 entérine ce choix.
Le 3 janvier 1915, Cholesky est détaché auprès du général commandant l'artillerie du 17ème corps d'armée pour l'organisation du tir. Le 11 février, il est affecté au Service Géographique de l'Armée pour être employé à un groupe de canevas de tir du détachement de l'armée des Vosges. Il rejoint son poste le 15 février. Il fut l'un des officiers qui comprit le mieux et développa le plus le rôle de la géodésie et de la topographie dans l'organisation des tirs d'artillerie. De nombreux documents relatifs à ces travaux se trouvent dans le Fonds A. Cholesky de l'École Polytechnique. Il fit, comme attaché à la commission d'étude dirigée par le Général Nourrisson, un certain nombre de conférences sur l'organisation du tir à des officiers d'artillerie (en mai 1915 avec le Capitaine de Fontanges puis à Saint Dié, en janvier 1916). Mais son activité ne se limitait pas là. Il s'intéressait également au repérage et à la surveillance des aéronefs, au point apparent d'émission des claquements des canons, à la photographie aérienne, aux appareils de pointage pour les mitrailleuses placées sur les avions Nieuport. Il rédigea de nombreux documents relatifs à ces questions ainsi que des rapports sur l'utilisation des canevas de tir, sur le but des groupes de canevas et la répartition du travail en leur sein, sur l'emploi des contre-batteries, sur le tir d'artillerie contre des batteries masquées, sur la correction de pointage en combat aérien, sur le travail de l'officier cartographe, etc. Il commence même à apprendre l'anglais. En juillet 1916, il devient chef du Groupe des Canevas de Tir de la VIIème Armée commandée par le Général de Villaret.
Cholesky est affecté, du 25 septembre 1916 à février 1918, à la mission militaire en Roumanie (entrée en guerre à côté des alliés à la fin août) par décision du Général Berthelot, Commandant en Chef. Il y rend d'éminents services en exerçant les fonctions de directeur technique du service géographique et, sur plusieurs documents officiels, il est fait état du grade de Lieutenant-Colonel. En avril 1916, il s'installe au Quartier Général de la IIème Armée à Bacau. Il organise complètement le service géographique de l'armée roumaine. De nombreux documents, souvent épais, relatifs a cette organisation se trouvent dans le Fonds A. Cholesky de l'École Polytechnique. On y voit les talents d'organisateur et le souci des détails manifestés par Cholesky.
Le 6 juillet 1917, Cholesky est promu Chef d'Escadron, c'est-à-dire Commandant. Le 17 décembre 1917, le Colonel J. Pavelescu, Chef du Service Géographique de l'Armée roumaine, le nomme Officier de l'Ordre Steaua României avec épées au cours d'un dîner d'adieu (sans doute à Jassy) offert à l'occasion du départ des Français de la Roumanie.
Le 5 juin 1918, il est affecté au 202ème Régiment d'Artillerie de Campagne qui fait partie de l'Armée du Général Mangin. Entre le 15 août et le 26 septembre, ce régiment participera à l'offensive sur la ligne Hindenburg qui passait par Lassigny, Ribécourt-Dreslincourt et Tracy-le-Mont. Les Allemands y avaient installé de nombreuses fortifications et aménagé des carrières, des postes de commandement, des observatoires, des abris, mais aussi des cimetières et des hôpitaux.
Le 202ème Régiment d'Artillerie de Campagne fut engagé dans des combats sur l'Ailette le 23 août et à Courson. Le 25 août, l'armée de Mangin s'apprête à rompre le front ennemi entre l'Aisne et Saint-Gobain.
Le 31 août 1918, le Commandant Cholesky décède à 5h du matin dans une carrière au nord de Bagneux (dans l'Aisne, à environ 10km au nord de Soissons) des suites de blessures reçues sur le champ de bataille. Il est inhumé au cimetière militaire de Chevillecourt près d'Autrèches dans l'Oise, à une quinzaine de kilomètres à l'ouest de Soissons. Le 24 octobre 1921 son corps sera transféré au cimetière de Cuts (dans l'Oise, à 10km au sud-est de Noyon), tombe 348, carré A.
La ligne Hindenburg sera percée le 2 septembre 1918, au cours de la seconde bataille d'Arras.
Cholesky était Officier du Nicham Iftikhar (10 juin 1907), Officier d'Académie (23 avril 1908), Chevalier de la Légion d'Honneur (10 avril 1915), titulaire de la Croix de Guerre avec palme, Officier de l'Étoile de Roumanie avec épées (17 décembre 1917), et décoré de l'Ordre de Saint Stanislas (6 août 1917) et du Nicham Medjidie.
Nous allons maintenant procéder à une description et à une analyse des différents manuscrits à caractère scientifique trouvés dans les papiers du Fonds A. Cholesky de l'École Polytechnique.
Le nom de Cholesky est passé à la postérité grâce à sa méthode de résolution des systèmes d'équations linéaires. Elle est toujours intensément utilisée de nos jours et c'est donc par elle que nous commencerons.
Voyons comment on arrive à un tel système d'équations.
Soit à résoudre le système d'équations linéaires Mx=c, où M est une matrice rectangulaire ayant m lignes et n colonnes. Si m
Selon l'échelle de la carte, il est nécessaire de tenir compte de la forme exacte de la terre. Les angles et les longueurs sont astreints à vérifier des équations de condition qui expriment le fait que la somme des angles d'un triangle doit être égale à une valeur connue (supérieure à 180 degrés pour tenir compte de la sphéricité de la terre), qu'en chaque point la somme des angles doit valoir 360 degrés et que les longueurs doivent rester les mêmes quel que soit l'ordre dans lequel les mesures sont effectuées (voir, par exemple, [30,17,29]).
Enfin, certains points géodésiques ne peuvent être observés qu'à distance et ne sont pas accessibles directement pour y installer les instruments de mesure. C'est, par exemple, le cas des clochers, des faîtes des constructions élevées ou des cheminées. Ainsi que l'écrit Cholesky [16, p. 264]
La compensation des réseaux géodésiques est due à Carl Friedrich Gauss (Braunschweig, 23 avril 1777 - Göttingen, 22 février 1855). Supposons avoir n mesures l1,...,ln de N quantités (angles ou distances) X1,...,XN. On veut les compenser, c'est-à-dire corriger les erreurs vi dont elles sont entachées à cause de l'imprécision des instruments et des inexactitudes expérimentales. Ces mesures li sont reliées aux N+n inconnues X1,...,XN et v1,...,vn par des fonctions non linéaires fi Appelons li* les mesures calculées pour des valeurs approchées Xi* en nombre restreint. Pour rendre linéaire le système ainsi obtenu, on effectue un développement de Taylor au premier ordre des fi. En notant A la matrice des dérivées partielles des fi par rapport aux Xj* , b le vecteur de composantes bi=li-li*, x celui des compensations xi=Xi-Xi* et v celui des vi, on trouve Ax=b+v. Résolvons ce système par la méthode des moindres carrés. Les erreurs vi sont des variables aléatoires normales centrées indépendantes et chaque li est une variable aléatoire d'écart-type si. La solution la plus probable est celle qui minimise
e2=p1v12+...+pnvn2 , avec pi=1/si2, ce qui se produit lorsque les dérivées partielles par rapport aux xj sont toutes nulles et conduit à ATPv=0, où P est la matrice diagonale des pi. C'est un système de N équations à n inconnues. Mais v=Ax-b et, donc, ATPAx=c en posant c=ATPb. Ce système, dit des équations normales, ne contient plus que les N inconnues x (voir [13] pour plus de détails).
Cholesky va chercher une matrice, L, triangulaire inférieure, telle que ce système s'écrive
LLTx=c. En posant y=LTx, ce système devient Ly=c. Sa résolution, simple puisque L est triangulaire, fournit y. Ce vecteur y étant calculé, on résout le système LTx=y, ce qui donne x.
La méthode des moindres carrés, également très utilisée en astronomie, conduit donc à la résolution d'un système d'équations linéaires dont la matrice est symétrique définie positive. Naturellement, les formules de Cramer en donnent la solution, mais une solution toute théorique puisque le volume des calculs les rendent rapidement impraticables. En effet, sur un ordinateur effectuant dix millions d'opérations arithmétiques par seconde, il faudrait quarante milliards d'années pour résoudre un système de dimension 23, c'est-à-dire beaucoup plus que l'âge de l'univers! Rapidement donc, les scientifiques se sont intéressés à des méthodes de factorisation de la matrice A en un produit de deux matrices. C'est le cas des méthodes de Gauss et de Cholesky.
Cholesky ne publia jamais ses travaux bien qu'il ait rédigé lui-même des rapports sur les opérations de nivellement de précision qu'il dirigeait en Algérie et en Tunisie [3] (voir aussi [4]). Une méthode nouvelle pour le calcul de la correction de mire y est donnée mais il est bien difficile d'y voir les prémices de sa méthode de factorisation.
La méthode de Cholesky fut, en fait, exposée pour la première fois dans une note de 1924 due au Commandant Benoît [10], de l'Artillerie Coloniale, ancien officier géodésien au Service Géographique de l'Armée et au Service Géographique de l'Indochine, Membre du Comité National Français de Géodésie et de Géophysique (il n'a pas été possible de trouver des renseignements biographiques plus précis sur lui). Benoît écrit
Nous suivrons, pour la démonstration de cette méthode, la progression même qui a servi au Commandant Cholesky pour l'imaginer.
On sait que la compensation d'un réseau géodesique a pour but de tirer des valeurs angulaires d'observation un système corrigé tel que toutes les vérifications de figures soient satisfaites et que la figure géométrique ainsi obtenue déforme aussi peu que possible celle que donneraient les valeurs d'observation.
Ces conditions de figure: fermeture des angles des différents triangles, égalités des longueurs obtenues pour un même côté quel que soit l'enchaînement suivi, donnent lieu à des équations dites de condition qui, développées par rapport aux corrections, peuvent être limitées au 1er ordre de petitesse.
On a, en somme, à résoudre un système de p équations linéaires entre les n corrections angulaires, devenues les véritables inconnues, n étant plus grand que p, sans quoi il serait inutile de procéder à des observations, le problème serait indéterminé. On s'impose la condition supplémentaire, déjà mentionnée, de déformer le moins possible la figure d'observation, c'est-à-dire de satisfaire aux équations avec les valeurs les plus petites possibles des inconnues.
On pourrait, pour cela, exprimer que la somme des valeurs absolues des inconnues est minima: mais cette condition ne se prête pas à une résolution algébrique commode et c'est la principale raison pour laquelle on préfère appliquer la méthode des moindres carrés de Legendre, qui donne d'ailleurs, en principe, le système correctif le plus probable...
L'article de Benoît se continue par le Résumé suivant
Enfin, il est intéressant d'en citer le dernier paragraphe
Mais cette adaptation est plus théorique que pratique, car elle entraîne à des calculs qui sont généralement plus longs que la résolution directe du système par une des méthodes habituelles: substitutions, éliminations, etc.. Elle a cependant deux avantages assez importants: d'une part celui de réduire les écritures, et, d'autre part, de constituer une méthode homogène, d'application brutale, présentant des vérifications continuelles.
L'article de Benoît se termine par un exemple numérique de compensation d'un quadrilatère par la méthode de Cholesky.
Donc, à cette époque, la seule trace de la méthode de Cholesky qui existait dans la littérature scientifique était cet article du Commandant Benoît.
Dans le Fonds A. Cholesky de l'École Polytechnique, cote B4, il existe un manuscrit de 8 pages 21.8x32 cm de Cholesky où cette méthode est parfaitement exposée. Il est intitulé Sur la résolution numérique des systèmes d'équations linéaires et porte la date du 2 décembre 1910. Ce manuscrit, contrairement aux autres manuscrits contenus dans le Fonds A. Cholesky, ne comporte presque pas de ratures. Seuls quelques mots sont rayés et remplacés par d'autres. On peut donc supposer qu'il ne s'agit pas là d'une première rédaction mais nous n'avons aucune indication sur la date réelle à laquelle Cholesky inventa sa méthode.
Cette note manuscrite de Cholesky constitue un travail d'analyse numérique complet et tout à fait remarquable pour l'époque (et même pour la nôtre): présentation et justification théorique d'un algorithme, étude de la disposition pratique des calculs sur une feuille de papier, discussion des problèmes posés par la mise en œuvre sur machine à calculer, étude des erreurs numériques dues à la précision finie des calculs, procédure de vérification des résultats et commentaires sur les essais numériques. De nos jours, la méthode de Cholesky est toujours d'une importance majeure. Une analyse mathématique détaillée de ce manuscrit est donnée dans [13].
On trouve dans le Fonds A. Cholesky de nombreux documents à caractère scientifique rédigés par Cholesky à l'occasion de ses activités pendant la guerre. Certains sont manuscrits et d'autres tapés à la machine. Ils montrent que leur auteur mit sa culture scientifique au service de l'armée.
Les documents militaires officiels (instructions, rapports, notes de service, etc.) ne comportent pas toujours de signature. Cependant, d'après le sujet et le style, il est à peu près certain que d'autres documents qui se trouvent dans le Fonds A. Cholesky lui sont dus. Par exemple, des corrections de la main de Cholesky se trouvent dans une Instruction sur l'organisation et les attributions des groupes de canevas de tir des armées, en date du 23 décembre 1915 et signée par Joffre.
Divers manuscrits relatifs au travail de Cholesky comme professeur à l'Ecole Spéciale des Travaux Publics, du Bâtiment et de l'Industrie (ESTP) se trouvent dans le Fonds A. Cholesky.
La planchette, ou goniographe, est un instrument capital en topographie et il en est largement fait mention dans les écrits de Cholesky. C'est un appareil qui sert à reporter sur une feuille, le canevas, les angles qui ont été mesurés par un goniomètre. L'alidade est un instrument de visée employé pour viser et tracer des directions. Il a été inventé par Archimède, au 3ème siècle. Il comporte une règle avec deux pinnules qui pivote sur un cercle gradué et qui est montée sur la planchette d'un goniographe. La règle comporte un biseau gradué le long duquel on trace le trait qui correspond à la direction de l'objet pointé. Dans l'alidade holométrique, inventée en 1667 par les français Adrien Auzout (Rouen, 28 janvier 1622 -Rome, 23 mai 1691) et Jean Picard (La Flèche, 21 juillet 1620 - Paris, 12 octobre 1682), cette visée s'effectue à l'aide d'une lunette comportant une règle à éclimètre. Elle est utilisée pour les levés à moyenne et grande échelle. Ces instruments nécessitent un ensemble de réglages délicats afin d'assurer une précision maximale aux mesures. Cholesky les a décrit largement dans ses divers cours de l'ESTP.
C'est un cours manuscrit de 239 pages intitulé Complément de Topographie et écrit sur des feuilles de 15.5x20 cm. Nous en possédons également une version en caractères d'imprimerie calligraphiés avec des corrections de la main de Cholesky. Donnons-en une table des matières succincte
C'est un cours manuscrit de 83 pages, sur des pages de 15.5x20 cm. En voici la table des matières
Il est intéressant de citer le début de l'Avant-Propos
L'exécution d'une telle épure est souvent compliquée et demande d'autant plus de soin que l'on désire une précision plus grande. Aussi n'a-t-on pas en général intérêt à chercher à résoudre graphiquement un cas isolé, pour lequel la construction du graphique demanderait le plus souvent beaucoup plus de temps que le calcul numérique.
Au contraire, les procédés du calcul graphique deviennent très avantageux lorsqu'il s'agit d'un calcul qui se reproduit très fréquemment, de l'application d'une formule dans laquelle les données seules varient. Le dessin peut alors être disposé de façon à fournir à l'aide d'opérations simples les résultats correspondants à tous les systèmes de valeurs des variables. L'établissement de l'épure peut dans ce cas être très long, il n'en résulte pas moins une économie de temps très sensible, si chaque fois qu'on s'en sert pour une opération très fréquente, on gagne une partie notable de la durée du calcul numérique qui se trouve ainsi supprimé.
Le calcul graphique s'applique donc principalement à des calculs qui doivent être répétés très fréquemment.
Il est inutile d'insister sur l'intérêt que présente toute réduction dans la durée des calculs, cette réduction se traduisant toujours par une économie de temps et par suite d'argent; c'est pour cette raison qu'on a cherché à réduire la durée des calculs numériques en calculant à l'avance des Tables numériques constituant absolument l'équivalent des épures employées dans le calcul graphique. L'avantage de ces dernières est que généralement elles sont plus faciles et moins longues à établir; de plus leur emploi est moins pénible pour le calculateur.
Nous possédons les pages 44 à 218 du manuscrit d'un livre de Cholesky intitulé Cours de Topographie et publié par l'École Spéciale des Travaux Publics à une date inconnue. Ce livre connut un succès certain puisqu'il eut au moins sept éditions. La septième édition, qui date de 1937, (Bibliothèque Nationale de France, cote 4-V-15365 (2)) fut revue par Henri-Albert Noirel, répétiteur à l'Ecole Polytechnique. Elle contient 442 pages, 100 figures et 18 planches ou photographies d'instruments.
En voici la table des matières
Le nom de Cholesky se retrouve dans certains ouvrages actuels de topographie. Sa méthode de résolution des systèmes d'équations linéaires y est citée en rapport avec la méthode des moindres carrés. Il est également fait mention du cheminement double de Cholesky dans [22]. Cette méthode de nivellement, que Cholesky mis en œuvre en Afrique du Nord à partir de 1910, consiste à mener simultanément deux cheminements distincts en plaçant la mire de nivellement successivement en deux points distincts situés en arrière puis en deux points situés à l'avant et ainsi de suite. On calcule ensuite séparément les deux cheminements et l'on compare les résultats obtenus.
Le Fonds A. Cholesky renferme également
• Un manuscrit de 15 pages avec le titre Instructions pour l'exécution des nivellements de précision. Il comporte 11 sections
• Un manuscrit de 8 pages intitulé Equation de l'ellipsoïde terrestre rapportée à Ox tangente au parallèle vers l'Est, Oy tangente au méridien vers le Nord, Oz verticale vers le zénith. Il en existe également un exemplaire à la machine à écrire dans lequel les formules mathématiques sont insérées à la main.
• Un manuscrit de 16 pages Étude du développement conique conforme de la carte de Roumanie. On! en possède aussi un exemplaire tapé à la machine où les formules mathématiques sont insérées à la main.
• Un manuscrit de 3 pages Instructions sur l'héliotrope-alidade (modèle d'étude 1905), écrit à La Charpenne le 18 août 1905.
• Cinq pages de description de l'alidade holométrique.
• Cinq pages de description de la boussole-éclimètre.
• Trois pages et trois plans sur la construction de lignes de chemin de fer.
• Trois pages intitulées Remarque au sujet du calcul de correction de mire.
• Divers cours et feuilles d'exercices destinés aux élèves par correspondance de l'ESTP.
• Deux feuilles avec le titre Compléments de Topographie. Levés d'études à la planchette. 5 séries et 2 exercices pratiques. Tâches à remplir. Ce document présente les idées de Cholesky sur le programme des études d'un cours de levés d'études à la planchette qu'il a donné à l'ESTP et que nous n'avons pas retrouvé (peut-être a-t-il été entièrement inclus dans son Cours de Topographie). Il se termine par
Il n'y a rien à ajouter !
Résoudre un triangle consiste, à partir de trois éléments, à calculer les trois autres. La longueur d'un côté doit toujours figurer parmi ces trois éléments. On a
La hauteur h sur le côté a (menée à partir de A) est
Signalons qu'en géodésie on mesure les angles non pas en degrés, comme en trigonométrie, ou en radians, comme en mathématiques, mais en grades, aussi appelés gons. Le cercle est divisé en 400 gons au lieu de 360 degrés.
Pour un triangle sphérique, la somme des angles est toujours supérieure à p. Des relations existent pour résoudre les triangles sphériques. Nous ne les donnerons pas ici.
Ces documents proviennent tous des Archives du Service Historique de l'Armée de Terre [1].
• Citation n. 561 à l'ordre du 17 ième Corps d'Armée
• Citation n. 344 à l'ordre de l'Armée du 12 octobre 1918
• Copie des notes du feuillet du personnel
Mai. Notes obtenues au cours régional de tir de la Courtine du 25 avril au 4 mai 1910: aptitude de l'officier au point de vue du tir, au début de la série: bien préparé - zèle et progrès constants, très satisfaisants - Aptitude à la fin du cours à remplir les fonctions de commandant de Compagnie: très apte à remplir au tir les fonctions de commandant de Compagnie.
Octobre. Le Capitaine Cholesky commande sa section avec beaucoup de zèle, de fermeté et de bienveillance; il a obtenu de très bons résultats qui pourront encore être améliorés par une surveillance plus serrée de certains détails. Très versé dans toutes les questions de tir, il tire avec calme et observe bien; il sera aux prochaines écoles de feu un des meilleurs tireurs du régiment. A donné, aux manœuvres de Picardie, toute satisfaction à son chef de groupe.
• 1911
Second brillant Capitaine et très bon tireur, ne négligeant aucun détail aussi bien dans l'administration que dans des questions d'instruction et d'entretien du personnel, le Capitaine Cholesky, qui vient d'être l'objet d'une mutation, pour le service géographique, quitte le régiment avec une connaissance parfaite à tous égards des fonctions de Capitaine.
• 1912
Octobre. Le Capitaine Cholesky a pris part aux manœuvres d'armée comme officier cartographe (État major du Général Marion); a mérité d'excellentes notes; officier remarquable en tous points. Proposé pour Chevalier de la Légion d'Honneur.
• 1913
Rayé des contrôles du Service Géographique le 25 mai 1913, mis hors cadre, à la disposition du Ministre des Affaires Étrangères (Chef du Service Topographique de la Régence de Tunis. Décision ministérielle du 4 juin 1913).
Rejoint le 23ème d'artillerie à Somme-Suippe (Marne) le 23 septembre; prend le commandement du 3ème groupe le 27 septembre, puis celui de la 9ème batterie le 18 octobre à l'arrivée du Chef d'Escadron Girard. Esprit très positif, très renseigné, très travailleur; a montré dès le début une grande activité aussi bien dans l'organisation de sa batterie et l'installation de ses bivouacs que dans la réalisation du tir contre avions ou le fonctionnement des observatoires: tire bien, observe bien - Chargé le 4 janvier 1915 de la confection du plan. Directeur du tir du C.A. [Corps d'Armée] et de la direction de l'observation du tir. Classé fin janvier au service géographique - Quitte le régiment au moment où il était en excellente situation soit pour l'avancement soit pour la Croix.
• 1915
Officier remarquablement doué, à l'esprit toujours en éveil, aux idées originales, le plus souvent fécondes dans leur application. A été pour le chef du groupe des canevas de tir de la 7ème armée un collaborateur parfaitement au courant de toutes les questions techniques, ardent à sa tâche. A contribué pour une grande part à tous les résultats obtenus. Très qualifié pour le grade supérieur.
• 1916
A dirigé avec compétence le G.C.T.A.. Travailleur, ingénieux, réfléchi, a développé largement la production du groupe et a pris des initiatives heureuses. En somme, a très bien servi dans la succession du Commandant Perrier.
• 1917
• 1918
A continué jusqu'au départ de Roumanie de la Mission Française à diriger avec autorité et compétence les services géographiques de l'armée roumaine. A acquis de par ces fonctions, tous les titres à exercer en France un emploi exigeant de l'initiative.
Ces relevés sont la transcription de ce qui est écrit dans le feuillet individuel de campagne. Seul s'y ajoute ce qui suit.
Proposé pour le grade de Chef d'Escadron avec le motif suivant:
Mérite grandement d'être nommé immédiatement au grade supérieur. 8 ans de grade de Capitaine ne feront pas de sa nomination un choix exceptionnel que mériterait cependant sa personnalité. Ardent, énergique, travailleur infatigable, ayant beaucoup d'autorité. Fait honneur à la Mission dans les fonctions dont il est chargé.
Nous reproduisons ici le début de la notice nécrologique rédigée en 1922 par le Commandant Benoît [5].
Le Commandant Cholesky
Ce fut fait deux ans plus tard et c'est grâce au Commandant Benoît que nous avons connaissance de la méthode de Cholesky.
Nous tenons à l'en remercier. Nous sommes redevables à Michela Redivo Zaglia, Professeur à l'Université de Padoue, Italie, dont l'aide dans la recherche de documents sur le web a été déterminante. Qu'elle en soit remerciée. Enfin, nous ne saurions oublier Monsieur Jean-Paul Devilliers pour sa lecture attentive de notre texte et ses remarques constructives.
[1] Dossier 126.454, Service Historique de l'Armée de Terre, Fort Vieux de Vincennes.
[2] Rapport sur les Travaux effectués en 1906, Cahiers du Service Géographique de l'Armée, n. 29, 1907.
[3] Rapport sur les opérations du nivellement de précision d'Algérie et de Tunisie pendant les campagnes 1910-1911, 1911-1912, 1912-1913 par le Capitaine Cholesky, Cahiers du Service Géographique de l'Armée, n. 35, 1913.
[4] Rapport sur les travaux effectués en 1912, Cahiers du Service Géographique de l'Armée, n. 36, 1913.
[5] Union Géodésique et Géophysique Internationale, Première Assemblée Générale, Rome, Mai 1922, Section de Géodésie, Bulletin Géodésique, 1 (1922) 159-161.
[6] R. Adrain, Research concerning the probabilities of the errors which happen in making observations, Analyst or Math. Muséum, 1 (1808)93-109.
[7] R. Adrain, Investigation of the figure of the earth and of the gravity in différent latitudes, Trans. Amer. Phil. Soc, 1 (1818)
[8] R. Adrain, Research concerning the mean diameter of the earth, Trans. Amer. Phil. Soc,
[9] R. Aublet, Historique des écoles d'artillerie, Bulletin d'Information et de Liaison des Officiers d'Artillerie d'Activé et de Réserve, 6 (1953) à 13 (1955).
[10] Cdt. Benoît, Note sur une méthode de résolution des équations normales provenant de l'application de la méthode des moindres carrés à un système d'équations linéaires en nombre inférieur à celui des inconnues, (Procédé du Commandant Cholesky), Bulletin Géodésique, 2 (1924) 67-77.
[11] A. Björck, Numerical Methods for Least Squares Problems, SIAM, Philadelphia, 1996.
[12] C. Brezinski, André Louis Cholesky, dans Numerical Analysis, A Numerical Analysis Conférence inHonourof Jean Meinguet, Bull. Soc. Math. Belg., 1996, pp. 45-50.
[13] C. Brezinski, La méthode de Cholesky, Rev. Hist. Math., à paraître.
[14] J.-P. Callot, Histoire de l'Ecole Polytechnique, Les Presses Modernes, Paris, 1959.
[15] J.-L. Chabert et al., Histoires d'Algorithmes, Belin, Paris, 1994.
[16] A. Cholesky, Cours de Topographie. 2è Partie, Topographie Générale, École Spéciale des Travaux Publics, Paris, 7è édition, 1937.
[17] L. Eyrolles, E. Prévôt, E. Quanon, Cours de Topographie. Livre I: Topométrie, Librairie de l'Enseignement Technique Léon Eyrolles, Paris, 1909.
[18] CF. Gauss, Theoria Motus Corporum Coelestium in Sectionibus Solem Ambientiem, Hambourg, 1809; Œuvres, t. VII, 1871; traduction française par E. Dubois, Paris, 1864.
[19] C.F. Gauss, Disquisitio de elementis ellipticis Palladis ex oppositionibus annorum 1803, 1804, 1805, 1807, 1808, 1809, Soc Roy. Sci. Göttingen, 1810; Œuvres, t. VI, 1874, pp. 3-24.
[20] C.F. Gauss, Theoria combinationis observationum erroribus minimis obnoxiae, deuxième partie, Soc Roy. Sci. Göttingen, 1823; Œuvres, t. IV, 1873, pp. 1-108; traduction française par J. Bertrand, Méthode des Moindres Carrés, Paris, 1855.
[21] H.H. Goldstine, A History of Numerical Analysis from the 16th through the 19th Century, Springer-Verlag, New York, 1977.
[22] P. Goix, Topographie, CRDP de l'Académie de Grenoble, Greboble, 2001.
[23] D. Guedj, Le Mètre du Monde, Éditions du Seuil, Paris, 2000.
[24] C.G.J. Jacobi, Uber eine elementare Transformation eines in Buzug jedes von zwei Variablen-Systemen linearen und homogenen Ausdrucks, J. Reine Angew. Math., 53 (1857) 265-270.
[25] W. Jordan, Handbuch der Vermessungskunde, 1873.
[26] A.N. Kolmogorov, A.P. Yushkevich, eds., Mathematics ofthe 19th Century. Mathematical Logic, Algebra, Number Theory, Probability Theory, Birkhäuser, Basel, 1992.
[27] J.H. Lambert, Anmerkungen und Zuäàtze zur Entwerfung des Land und Himmelscharten, 1772
[28] A.M. Legendre, Nouvelles Méthodes pour la Détermination des Orbites des Comètes, Paris, 1805.
[29] P. Merlin, La Topographie, Collection Que-Sais-Je? , vol. 744, 2è éd., Presses Universitaires de France, Paris, 1972.
[30] P. Pizzetti, H. Noirel, Géodésie, dans Encyclopdédie des Sciences Mathématiques Pures et Appliquées, Édition Française, J. Molk et Ch. Lallemand éds., Tome VI, Volume 1, Gauthier-Villars et Cie, Paris et B.G. Teubner, Leipzig, 1916, rééedition par Jacques Gabay, Paris, 1993.
[31] G.W. Stewart, Gauss, statistics, and Gaussian élimination, dans Computing Science and Statistics: Computationally Intensive Statistical Methods, J. Sali and A. Lehman eds., Interface Foundation of North America, Fairfax Station, VA, 1994, pp. 1-7.

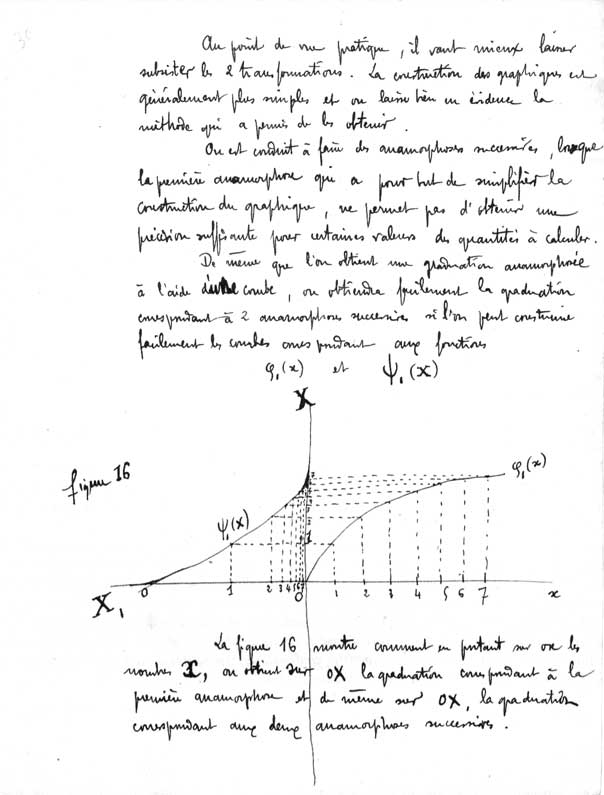
Page du "cours de calcul graphique" de Cholesky
Archives de l'Ecole polytechnique (Fonds A. Cholesky)
Toutes les fois que l'on fait une triangulation calculée, il y a avantage à faire également une compensation par le calcul. On est alors amené à écrire un certain nombre d'équations représentant les relations géométriques entre les divers éléments des figures de la triangulation et comme il y a généralement plus d'inconnues que d'équations, on lève l'indétermination en écrivant que la somme des carrés des corrections est minima.
2.1.2 La contribution de Cholesky
Le Commandant d'Artillerie Cholesky, du Service géographique de l'Armée, tué pendant la grande guerre, a imaginé, au cours de recherches sur la compensation des réseaux géodésiques, un procédé très ingénieux de résolution des équations dites normales, obtenues par application de la méthode des moindres carrés à des équations linéaires en nombre inférieur à celui des inconnues. Il en a conclu une méthode générale de résolution des équations linéaires.
Résumé. - En somme, les calculs très complexes par les méthodes ordinaires, y compris celle de Gauss, et qui nécessitent autant de tableaux distincts que d'inconnues à éliminer, d'où une complication d'écriture extrême, deviennent, par la méthode Cholesky et l'emploi de la machine à calculer, relativement aisés et beaucoup plus courts. Ils sont présentés sur un seul tableau, où l'ordre de formation est facile à reconnaître et où les opérations sont toujours les mêmes. On peut, avec cette méthode, aborder facilement des résolutions à 40 ou 50 inconnues, qui auraient demandé des semaines de travail ardu par les procédés antérieurs.
Application de la méthode Cholesky à la résolution d'un système de p équations linéaires à p inconnues. - Le système étant déterminé, n'a qu'une solution unique, que l'on obtiendra par suite, également, en recherchant la solution minima fournie par l'application de la méthode des moindres carrés. Le procédé de calcul du Commandant Cholesky peut dès lors s'adapter à la résolution d'un système d'équations linéaires quelconques.
[Cholesky utilisait des machines à calculer de type Dactyle qui furent construites par l'entreprise Château jusqu'au début des années 1950. Elles avaient été inventées par l'ingénieur suédois Willgodt Theophil Odhner vers 1878. Le brevet étant tombé dans le domaine public en 1906, de nombreuses copies furent alors fabriquées dans le monde entier.]
2.2 Documents militaires
2.2.1 Manuscrits
• Canevas de tir pour situer le plus exactement possible la ligne de combat (2 p.).
• Surveillance des aéronefs (1 p.).
• Protection contre les incursions des aéronefs (1 p.).
• Lieu du point apparent d'émission du claquement pour une pièce de 77 du Grafen Wald pour la Section B, quand on fait varier le plan de tir de la pièce (1 p. et 3 p. de brouillon).
• Tenue à jour du programme de la photo aérienne (2 p.).
• Appareil de pointage pour mitrailleuse sur avion Nieuport (3 p.).
• But du groupe de canevas de tir (2 p.).
• Canevas de tir pendant la marche en avant (5 p.).
• Instructions particulières à l'artillerie pour l'emploi des contrebatteries (complément à l'ordre général no. 12).
• Instructions pour la surveillance des aéronefs (1 p.).
• Étude d'artillerie (1 p.).
• Projet de répartition du travail dans le GCTA (3 p.).
• Manuscrit sans titre sur le travail de l'officier géographe (5 p.).
• Manuscrit sans titre sur les repérages par avions (3 p.).
• Manuscrit sans titre avec des calculs numériques sur les arrangements (1 grande double page).
• Sur le combat aérien (10 p.).
• Organisation du tir de l'artillerie (36 pages dactylographiées). Il s'agit des conférences faites par Cholesky et le Capitaine de Fontanges en mai 1915.
2.2.2 Documents imprimés
• Étude sur le tir d'artillerie contre les batteries masquées (envoyé le 5 novembre 1914 depuis Somme-Suippe au Chef d'Escadron Girard, commandant le 3ème groupe du 23ème Régiment d'Artillerie).
• Projet d'organisation de l'observation et du tir d'artillerie sur un front de Corps d'Armée (24 décembre 1914).
• Opérations topographiques effectuées par l'artillerie pour relever les batteries et leurs repères.
• Notes sur le tir avec observateurs latéraux et aériens (avril 1915).
2.3 Cours de l'ESTP
2.4 Complément de Topographie
Chapitre I Généralités
Chapitre II Plans de topographie détaillée
Étude complète d'un levé au 1/1000e
Exécution du levé
Piquetage et repèrement des points du canevas
Levé du canevas
Stations de planchette. Construction du canevas
Nivellement
Levé des détails
Nivellement des détails
Chapitre III Levé à la boussole. Éclimètre
Chapitre IV Triangulation graphique
2.4.1 Cours de Calcul Graphique
Avant-Propos
Chapitre I Généralités
Représentation graphique des nombres
Courbes - Diagrammes - Équations à 2 variables
Surfaces - Équations à 3 variables
Chapitre II Abaques
Abaques à deux variables
Théorie générale des abaques
No. 1 - Définition du calcul graphique - Son utilité
Le calcul graphique a pour objet de remplacer les calculs numériques par un dessin, une sorte d'épure, dont la construction permet de passer directement des données au résultat. L'épure employée est généralement désignée sous le nom d'Abaque.
2.4.2 Cours de Topographie
Première Partie Considérations générales
Chapitre I Définitions - De l'échelle
Chapitre II Particularités des cartes de topographie générale
Chapitre III Erreurs - Fautes
Deuxième Partie Instruments
Chapitre IV Caractéristiques des instruments de topographie générale
Chapitre V Instruments pour la mesure des longueurs
Chapitre VI Instruments pour la mesure des angles
Chapitre VII Instruments pour l'établissement et l'emploi des perspectives
Chapitre VIII Instruments pour la détermination des altitudes
Chapitre IX Accessoires
Troisième Partie Étude des levés
Chapitre X Méthode générale
Chapitre XI Plans de topographie générale
Chapitre XII Cartes chorographiques
Chapitre XIII Levés hydrographiques
Chapitre XIV Levés par les perspectives
2.5 Autres manuscrits
• Trois pages intitulées Sur la détermination des fractions de secondes de temps.
I Conditions des nivellements à effectuer en dehors des grandes voies de communication
II Reconnaissance du tracé
III Repèrements
IV Repères fixes et provisoires
V Installation de niveau
VI Réglage du niveau
VII Mires
VIII Exécution d'une nivelée
IX Tenue des carnets
X Calculs à effectuer sur le terrain
XI Calculs définitifs
Recommandation très importante. L'élève se tromperait beaucoup s'il croyait trouver dans les cours qu'il a entre les mains les solutions complètes des exercices qui lui sont proposés. Ces exercices ont pour but principal de le forcer à réfléchir, de l'empêcher d'apprendre ses cours trop strictement, en lui indiquant que dans un travail aussi complexe qu'un levé topographique, tout dépend de la valeur de l'opérateur qui doit par suite être habitué à raisonner toutes ses opérations. Aussi l'élève aura-t-il souvent avantage, lorsqu'il sera arrêté par un exercice à abandonner l'étude du cours et à chercher simplement si le bon sens ne lui indiquera pas la solution. Les exercices corrigés constitueront un complément indispensable du cours, et non pas une répétition; aussi l'élève ne devra-t-il pas se décourager s'il rencontre des difficultés sérieuses dans les exercices qui lui sont proposés. Qu'il montre qu'il sait réfléchir, on ne lui en demandera pas davantage.
Appendice 1
A+B+C=n
a/sinA=b/sinB=c/sinC
a²=b²+c²-2bc cosA
(a+b)/(a-b)=tg((A+B)/2)/tg((A-B)/2).
Données Calcul des autres éléments
a,A,B C=p-A-B, b=a sin B/sin A, c=a sinC/sin A
a,b,C tg(A-B)/2={a-b)/{a+b) ctg C/2, (A+B)/2=(p-C)/2
Ayant obtenu A+B et A-B, on en déduit A et B
c=a sinC/sin A
a,b,A sinB=b sin A /a
Si a>b, B<p/2 ne peut prendre qu'une seule valeur.
Si a
2 - si b sin A=a, B=p/2,
3 - si b sin A > a, le triangle est impossible.
C=p-A-B, c=a sinC/sin A
a,b,c r² =(p-a){p-b){p-c)/p avec p=(a+b+c)/2
tg A/2=r/(p-a), tg B/2=r/(p-b), tg C/2=r/{p-c)
Appendice 2
Documents militaires
Citations
• Citation n. 148 à l'ordre de la IV ième Armée le 21 décembre 1914 (J.O. du 14 janvier 1915)
Le Général commandant la IVème Armée cite à l'ordre de l'armée pour les faits suivants: le Capitaine Cholesky André: Envoyé le 8 décembre auprès du Lieutenant-Colonel directeur des attaques du 83ème, pour lui indiquer le moment où l'attaque pouvait se déclencher; sa mission terminée est resté volontairement auprès de cet officier supérieur pour lui servir d'adjoint, et, sous un feu intense, a fait ce service jusqu'au lendemain neuf heures, dans nos tranchées et dans les tranchées ennemies dont on venait de s'emparer. Officier d'Artillerie exceptionnellement doué, dont les multiples observations ont puissamment contribué depuis un mois a donner à notre artillerie une supériorité complète sur l'artillerie ennemie.
Le Général commandant l'artillerie cite à l'ordre de l'artillerie du 17ème Corps d'Armée le Capitaine Cholesky du 23ème Régiment d'Artillerie pour le motif suivant: a fait preuve d'activité, d'initiative, et de talent en organisant la centralisation dans l'artillerie du 17ème Corps d'Année des services des transmissions, de l'observation et du tir.
Officier de la plus haute valeur par sa science, son mépris absolu du danger et le haut exemple donné à tous. A imprimé à son groupe une impulsion irrésistible. Tué à son poste de combat.
Feuillet individuel de campagne
• Résumé des notes antérieures à l'année 1910
Sorti de Fontainebleau avec le n. 4 sur 92 en 1898. Se présente bien, sert avec zèle et entrain, un peu étourdi, monte bien à cheval. Deviendra un bon officier.
Détaché au service géographique de l'armée en Tunisie en 1902, 1903-04-05 à titre temporaire, est définitivement affecté à ce service le 24 janvier 1905. Très bien noté. Nommé Capitaine le 25 mars 1909, il est affecté au 13ème Régiment d'Artillerie par décision ministérielle du 28 août suivant. Bonne impression dès le début.
Le Colonel Grand-Didier.
• 1910
Avril. Tempérament robuste, intelligence vive, esprit net et réfléchi. Caractère très franc, bienveillant et ferme, le Capitaine Cholesky s'occupe avec beaucoup de soin de l'instruction et de l'administration de sa Compagnie. Bien qu'ayant été longtemps détaché, s'est mis rapidement au courant du service de la troupe. Connaît très bien son personnel. Fera un très bon Capitaine.
Le Colonel Grand-Didier.
Le Chef d'Escadron Vincent, Directeur de l'instruction militaire à l'École Polytechnique, Directeur du cours.
Le Colonel Grand-Didier.
Avril. Esprit méthodique, très réfléchi, le Capitaine Cholesky a du calme, du sang-froid, et beaucoup d'initiative. La batterie est bien tenue, bien instruite et bien administrée. Il commande d'une façon brillante sa batterie au tir; il observe sûrement et a la décision prompte.
Le Colonel Grand-Didier.
Le Lieutenant Colonel [illisible].
Classé à l'État major particulier de l'artillerie pour être détaché à la Direction du Service Géographique par décision ministérielle du 24 septembre 1912.
Avril. Arrivé au Service Géographique de l'armée au mois d'octobre, le Capitaine Cholesky a été classé à la section de Géodésie où il avait déjà été apprécié de 1905 à 1909. Chargé de la direction des opérations de nivellement de précision en Algérie et en Tunisie, il a rempli ses fonctions avec une autorité et une compétence remarquables. Esprit scientifique, toujours en éveil et au travail.
Le Chef d'Escadron, Chef de la Section de Géodésie, Lallemand.
Le Lieutenant Colonel, Chef de la Section de Géodésie, Lallemand.
Avril. A continué à diriger les opérations du nivellement de précision en Algérie et en Tunisie avec un zèle et une compétence remarquables; parait devoir obtenir une place à la Direction des Travaux Publics du Gouvernement Tunisien, comme chef du service topographique. Le Service Géographique et l'armée ne pourront que regretter son départ, les officiers de cette valeur étant rares.
Le Lieutenant Colonel, Chef de la Section de Géodésie, Lallemand.
Lallemand.
• 1914
A été affecté à un emploi de Capitaine au 7ème groupe d'artillerie à pied de Bizerte, en cas de mobilisation. A commandé la lOème batterie du dépôt depuis son arrivée au corps. Affecté au 16ème Régiment d'Artillerie de Campagne (dépôt d'Issoire). Dirigé le 15 septembre sur son nouveau poste. Tel. 119ms du Général Commandant en chef des troupes de l'Afrique du Nord. Reçu le 10 septembre.
Bizerte, le 13 septembre 1914. Le Commandant du 7ème groupe, L. Viane [ ? ].
Le Lieutenant Colonel Malet.
10 février 1915. Le Capitaine Cholesky a fait preuve d'une connaissance très complète de tout ce qui concerne l'organisation du tir, de l'observation et du service des transmissions. Il a déployé une activité et un talent d'organisation remarquables dans le courant de janvier et jusqu'au moment de son départ.
Le Général commandant l'artillerie du 17ème C.A., Falque.

Gabriel Paul Vincent Falque, ici élève de la promotion 1878 de Polytechnique, devint général de division
(C) Photo Collections de l'Ecole polytechnique
Le Général de Boissoudre, Chef E.M. 7ème armée.
Pendant le 1er semestre 1916, le Capitaine Cholesky a continué à faire preuve des mêmes qualités. Il prend aujourd'hui le commandement du groupe des canevas de tir de la 7 ième armée pour lequel il est parfaitement qualifié. Il devra toutefois se méfier comme chef de service de quelque tendance à l'originalité et au paradoxe. Il doit être laissé le moins longtemps possible dans le grade de Capitaine, les officiers de sa valeur étant rares. Il figurera partout, dans un service technique comme dans la troupe avec éclat et honneur.
Le Chef d'Escadron, chef du groupe des canevas de tir, Perrier . Le 26 mai 1916.
Le Lieutenant Colonel Hergault, chef d'E.M. 7ème Armée, le 24 octobre 1916.
Directeur Technique du Service Géographique en Roumanie, a pris dès son arrivée la haute main sur ce service secouant les torpeurs, triplant la production et assurant la continuité du travail malgré le transfert des services par suite des opérations. Fait honneur au Service Géographique français, actif, énergique, homme d'autorité, a trouvé ici le plein développement de sa personnalité. Sa nomination, déjà tardive, ne doit plus être différée.
Au GQG roumain, le 25 janvier 1918, le Colonel Pétin, chef d'E.M..
Mêmes excellentes notes.
Le chef d'E.M. Pétin.
Le chef d'E.M. Mission Roumaine, Colonel V. Pétin.
Relevé des notes
Le Général Berthelot, Chef de la Mission Militaire en Roumanie.
Appendice 3
André-Louis Cholesky, né le 15 octobre 1875 à Montguyon (Charente-Inférieure), entra à l'École Polytechnique à l'âge de vingt ans et en sortit dans l'arme de l'Artillerie. Affecté à la Section de Géodésie du Service géographique, en juin 1905, il s'y fit remarquer de suite par une intelligence hors ligne, une grande facilité pour les travaux mathématiques, un esprit chercheur, des idées originales, parfois même paradoxales, mais toujours empreintes d'une grande élévation de sentiments et qu'il soutenait avec une extrême chaleur.
C'était l'époque où la révision de toute la triangulation française venait d'être décidée pour faire suite à la révision de la Méridienne de Paris et pour servir de base à une nouvelle triangulation cadastrale. Le problème de la compensation des réseaux préoccupait bon nombre d'officiers de la Section, désireux de contribuer à fixer dans le sens de la rapidité, de la commodité et de la précision maxima, des méthodes qui n'étaient pas encore entièrement arrêtées. Cholesky aborda ce problème en apportant dans ses solutions, comme dans tout ce qu'il faisait, une originalité marquée. Il imagina pour la résolution des équations de condition par la méthode des moindres carrés un procédé de calcul très ingénieux qui rendit aussitôt de grands services et qu'il y aurait certes avantage pour tous les géodésiens à publier un jour.
Références