La Mathématique d'Ampère est restée à l'ombre du monument que constituent les théories de l'électromagnétisme et de l'électrodynamique. N'eussent été l'étendue et la profondeur de la culture mathématique de leur inventeur, ce dernier n'aurait probablement pas partagé avec le seul Lord Kelvin la gloire d'avoir donné son nom à l'une des sept unités de base du Système International.
L'originalité de l'œuvre réside plus dans l'inventivité et la virtuosité dans la conduite du calcul, comparables à celles d'un Gauss ou d'un Euler, que dans l'apport à la science mathématique. La rareté des références à l'écrit peut donner une fausse idée de l'abondance de ce dernier dont, il est vrai, une grande partie est restée inachevée ou non publiée.
Archivés à l'Institut, à l'École polytechnique ou à l'Académie de Lyon, certains de ces documents, oubliés, apparaîtront à l'occasion de la présentation anecdotique de quelques uns des travaux qui ont marqué la carrière de mathématicien d'Ampère.
1782 : Le jeune André Marie quitte, à l'âge de sept ans, les quais de la Saône qui l'ont vu naître pour la propriété familiale de Poleymieux. Dans ce village de quatre cents âmes, sans école jusqu'en 1833, le père Jean-Jacques, un bourgeois cultivé, a l'inconscience d'appliquer à l'enfant les préceptes éducatifs de l'Emile, lui laissant le libre choix de ses sujets d'étude.
Si l'on en croit l'une des autobiographies d'Ampère, la lecture s'apprend en solitaire chez Buffon, dans les tomes de l'Histoire Naturelle consacrés aux oiseaux et publiés à partir de 1770. Les autres précepteurs, ce sont les ouvrages de la bibliothèque encyclopédique constituée par son père. L'envoûtement par l'Abrégé des Élémens de Mathématiques de Rivard ouvre la voie aux Traités des sections coniques du marquis de l'Hospital (1720), et de De la Chapelle (1750), suivis des Élémens d'algèbre de Clairaut (1749). Le latin, enseigné très tôt par son père, rendait accessibles les écrits des Bernoulli et d'Euler.
En 1793, son père procure à André Marie la Méchanique Analytique de Lagrange (1788). L'étude de l'ouvrage de celui qui restera son Maître à penser le passionnera à un point tel qu'il vivra en dehors de la tragédie familiale jusqu'à la révélation de la mort de son père sur la guillotine. La lecture des 21 infolio de l'Encyclopédie sera achevée en quelques années, ce qui donne la mesure de la capacité d'absorption du lecteur pourtant handicapé par une désastreuse myopie. La découverte fortuite des lunettes n'y mettra fin qu'à l'âge de 19 ans.
Lors des premiers contacts avec l'Encyclopédie, la rencontre des symboles de la differentiation avait plongé le jeune garçon dans un abîme de perplexité. Son père avait alors sollicité de l'un de ses amis, l'abbé Daburon, l'enseignement de quelques leçons de calcul différentiel. On peut retrouver, dans les archives de l'Académie des sciences, le texte de ces leçons commencées le 9 avril 1788. Outre le calcul différentiel et intégral, elles portent sur la géométrie analytique et infinitésimale et n'ont, à l'époque, rien à envier au programme du taupin du 20e siècle.
Muni de ce viatique, le jeune Ampère va faire son entrée dans le monde des mathématiciens.
Lors de la séance du 8 juillet de cette même année 1788, le Secrétaire perpétuel de la Classe des sciences à l'Académie de Lyon fait part « d'une lettre et d'un mémoire de M. Ampère fils, âgé de 13 ans, qui prie l'Académie de lui donner son avis sur ce mémoire dans lequel il prétend avoir résolu le fameux problème de la quadrature du cercle. » Un mathématicien, l'abbé Roux, accepte d'en faire un commentaire à titre privé. L'Académie de Lyon avait en effet décidé le 19 août 1783, à la suite de celles de Paris en 1775 et de Berlin en 1776, de refuser toute communication sur le sujet.
Aucune trace n'a été retrouvée de ce mémoire, non plus que de son envoi et du commentaire attendu. Il a par contre subsisté une page autographe, application immédiate des leçons de géométrie infinitésimale de Daburon, où est proposée une construction de la rectification d'un arc de cercle. Un peu hâtivement peut-être, on a attribué à cet unique feuillet le titre de "Mémoire" et nié l'existence de celui sur la quadrature. L'argument qu'il n'en avait été présenté qu'un seul est presque certain ; par contre, celui qu'il avait pu y avoir confusion, dans l'esprit du rapporteur, entre les termes "quadrature" et "rectification" apparaît peu vraisemblable. Il n'est pas interdit d'envisager le tiers exclu, où le feuillet survivant aurait pu faire partie d'un mémoire disparu sur la quadrature du cercle, dont le développement de la circonférence constituait la clef depuis Archimède. André Marie a lu dans Rivard cette démonstration, par une intégrale qui ne dit pas encore son nom, que l'aire du cercle est égale à celle d'un triangle rectangle dont les côtés sont respectivement la longueur et le rayon de la circonférence. Ne reste plus alors qu'à construire la moyenne proportionnelle entre ces deux segments.
Le même Rivard avait certes écrit : « Il y a tant de géomètres...qui ont cherché inutilement la quadrature du cercle, que c'est une témérité insupportable à des commençants d'espérer de la trouver ». Cette sentence aurait pu apparaître un défi chez un jeune garçon qui manifestait une assurance en singulier contraste avec l'extrême timidité affichée tout le reste de son existence. En témoigne une lettre adressée à M. de La Baume où l'auteur, qui allait avoir 16 ans, critique le "Paradoxe d'Euler". Cette missive est reproduite au début de l'ouvrage de Louis De Launay : Correspondance du Grand Ampère.
Son ami Arago dira d'Ampère : « Sa vocation était de ne pas être professeur ». C'est pourtant par des cours particuliers d'algèbre et d'astronomie qu'il commence sa carrière en septembre 1797. Celui que son contrat de mariage du 7 août 1799 avait étiqueté "Mathématicien" sera, à 26 ans, membre de l'Académie de Lyon à laquelle il aurait soumis en 1801 le mémoire : Démonstration de l'égalité des polyèdres symétriques. Le 24 décembre 1801, lors de la Consulte de la République cisalpine réunie à Lyon par Bonaparte, il prononce un discours à l'Académie. Dans le droit fil de la Méchanique Analytique, l'orateur annonce une théorie qui ramène "les propriétés des fluides électriques et magnétiques à celles de la mécanique des fluides élastiques". L'ouvrage correspondant ne sera jamais publié.
En février 1802, remarqué par les autorités scientifiques en dépit de son statut d'autodidacte, Ampère sera nommé professeur de physique et de chimie à l'École centrale de Bourg-en Bresse ; poste qui sera agrémenté de leçons dans une institution privée. L'arrêté de Bonaparte, en date du 4 avril 1803, nommera «le citoyen Ampère professeur des 3e et 4e classes de mathématiques au lycée de Lyon ». Le nouveau promu rejoindra son poste trois mois avant le décès de son épouse. Fin 1804, les mémoires rédigés à Bourg ouvriront à Ampère les portes de Polytechnique sur la recommandation de Delambre.
Étant donné son endettement permanent, Ampère devait impérativement ajouter à ses cours d'Analyse à l'École des charges de subsistance. En 1808 d'abord celle, très contraignante, d'Inspecteur général de l'Université. Le 28 novembre 1814 enfin, c'est l'élection à l'Institut au fauteuil de l'abbé Bossut. L'année précédente, la candidature au siège de Lagrange, mort en avril 1813, avait rencontré un échec. Contraint d'abandonner la chimie à laquelle il se vouait entièrement depuis 1807, Ampère avait dû rédiger, à plume forcée, trois mémoires sur les équations aux différentielles partielles. Ironiquement, c'est ce travail à contrecœur qui est universellement cité dans les traités classiques d'Analyse. N'eût été l'obligation de cette tâche, Ampère serait peut-être plus connu, hormis les spécialistes, comme chimiste que comme mathématicien. Il quittera l'École en 1824 pour le Collège de France où il professera la physique expérimentale.
Dès son arrivée à Bourg le 17 février 1802. Ampère n'a qu'une idée en tête : produire un mémoire qui lui vaudra une nomination à Lyon. Il a dû, en effet, laisser à Lyon sa femme qui se meurt tout doucement à la suite de la naissance de leur fils le 12 août 1800.
Le 27 avril 1802, il écrit : «Il y a sept ans que je m'étais proposé un problème de mon invention, que je n'avais point pu résoudre directement... (*) ». Il ajoute, dans l'euphorie de la solution révélée « qu'une publication d'une vingtaine de pages devrait lui assurer une chaire dans un lycée ». Inconscient, il pensait terminer en moins d'une semaine un ouvrage qui, soumis au jugement de Lalande, restera 8 mois sur le métier. Né à Bourg en 1732, Lalande avait voué une solide amitié au jeune professeur et lui avait suggéré le complément de quelques applications numériques. Vexé par cette proposition, Ampère avait émis des doutes sur la capacité du vieil astronome à comprendre son travail. Lors de la séance de la Société d'émulation et d'agriculture de l'Ain, le 8 août 1802, Lalande en avait cependant présenté un rapport élogieux qui avait valu à Ampère son admission à la Société.
L'accusé de réception du mémoire, présenté à l'Institut le 12 janvier 1803, comporte une annotation de Laplace que la Classe avait désigné comme rapporteur. Elle signale un oubli dans la discussion de la convergence d'une série. Catastrophé, Ampère doit procéder d'urgence à une rectification mais, comme toujours, l'éditeur, son beau-frère Périsse, devra attendre les corrections qui ne parviendront qu'en avril à l'Institut. La brochure d'une vingtaine de pages en comportera finalement 63 que l'on peut comparer au morceau de virtuosité d'un candidat au concours du Conservatoire. Les termes d'une série s'y développent parfois, de façon implacable, sur une page entière en format paysage et il fallait toute la candeur d'Ampère pour espérer un succès en librairie. En 1995, un éditeur bien connu avait pourtant annoncé une réédition. Le titre n'est pas apparu dans ses catalogues ultérieurs et on recherche vainement des références à ce mémoire.
Après un rappel des travaux de Buffon sur le jeu, le préambule annonce la publication prochaine d'un ouvrage sur les séries, rédigé en commun avec son ami François Clerc qui enseigne les mathématiques dans le même établissement. Les Leçons élémentaires sur les séries et autres formules indéfinies ne seront pas publiées. En subsistent toutefois plusieurs cahiers autographes conservés aux archives de l'Académie des sciences.
On entre dans le vif du sujet avec la définition du cas d'un joueur qui risque, à chacune d'un nombre illimité de parties, une aliquote 1/m de sa fortune. La variable q est définie comme le rapport de la probabilité de gain q/1+q à celle 1/1+q de perte. Dans l'hypothèse du gain de p parties, le joueur sera ruiné s'il en perd m+p et la probabilité de cette occurrence est donnée par :
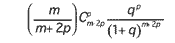
Le premier facteur résulte de l'élimination de tous les cas qui auraient conduit à une ruine prématurée avant la partie de rang m+2p considérée.
Dans sa recherche de la certitude de cette ruine, Ampère pose le problème de la convergence de la série ci-dessus. Appliquant la règle de d'Alembert, il trouve qu'il en est ainsi, à partir d'un certain rang, si p> (m²-3m+2)/6 , un gage de longévité pour le joueur si la partie aliquote 1/m est petite. La série converge effectivement vers 1 lorsque q<1, mais vers 1 lorsque q>1, cas oublié par Ampère. À ce point du mémoire, la rédaction marque une cassure qui témoigne de l'effet dévastateur qu'avait eu la remarque de Laplace. En accord avec les prémisses de 1795, sont étudiés ensuite le cas du jeu de quitte ou double et celui où s'affrontent deux joueurs de fortunes inégales. Un appendice est dédié à la démonstration que la formule du binôme peut se mettre sous la forme d'un développement suivant les puissances du produit et de la somme des arguments. Ces 14 dernières pages ne constituent pas la partie la moins intéressante du mémoire.
Après son retour à Lyon, Ampère conservera des relations privilégiées avec la Société d'émulation. Le 30 décembre 1803, y est présenté le Mémoire sur les avantages qu'on peut retirer dans la théorie des courbes de la considération des paraboles osculatrices, avec des réflexions sur les fonctions différentielles dont la valeur ne change pas lors de la transformation des axes.
Le 2 février 1803 est soumis à la Société d'émulation, en présence de Delambre, le Mémoire sur l'application des formules générales du calcul des variations aux problèmes de la Mécanique. La publication, à ce moment là, de ce « petit mémoire » dont la rédaction avait été commencée l'année précédente à Lyon, était surtout motivée par la nécessité d'affermir le crédit de son auteur auprès de Delambre. Quoi qu'il en soit, il s'agit peut-être là de l'œuvre la plus inattendue d'Ampère en ce qu'elle présente une critique de l'ouvrage qui l'a accompagné toute sa vie. Lagrange avait prôné la nécessité de s'affranchir dans les mathématiques de toute "hypothèse métaphysique" et, dans l'introduction à sa Méchanique Analytique, tirait fierté d'avoir ramené la mécanique à un chapitre de l'analyse. Ampère, quant à lui, écrivait : « Ce qu'on appelle un fait d'analyse doit toujours être ramené, si l'on veut s'en faire une idée juste, aux principes métaphysiques de cette science ». Suit le projet, « que le sujet du mémoire ne permet pas d'examiner », de repenser les fondements même du calcul des variations « dont la théorie générale n'est pas encore établie sur des bases absolument rigoureuses ». En outre, est critiqué d'entrée le fait de « recourir sans cesse à cette fastidieuse intégration par parties ».
Lors des leçons de 1788, Ampère avait été soumis par l'abbé Daburon à la question de la brachistochrone dont Jean Bernoulli avait publié la solution dans les Acta Eruditorum de Leipzig en juin 1696. La démonstration repose sur l'analogie, exotique, entre la trajectoire d'un point matériel pesant et celle d'un rayon lumineux. Bien qu'il ne fasse appel qu'au principe de Fermat et au théorème des forces vives, le mémoire de Jean Bernoulli peut être considéré commme l'acte de naissance du calcul des variations. Ampère avait probablement lu le : Methodus inveniendi... où Euler expose en 1744 son étude des géodésiques. La méthode consiste à inscrire entre les points extrêmes de la courbe recherchée une ligne polygonale représentée par une équation aux différences finies. La recherche d'une extrémale de la fonction y(x) ainsi discrétisée conduit à l'équation différentielle :
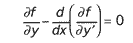
Depuis la recherche du solide de moindre résistance par Newton en 1687, la solution de tous les problèmes d'extremum qui s'étaient posés jusqu'alors, reposait sur la détermination d'une fonction y(x) qui rende minimale la valeur d'une intégrale définie telle que :
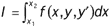
Lagrange introduira en 1760 le concept de variation d'une équation fonctionnelle et l'opérateur variationnel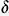 
. La propriété de commutativité avec les opérateurs de dérivation et d'intégration autorisera, dans la recherche de l'extremum, le recours à l'intégration par parties décrié par Ampère. Lagrange retrouvera ainsi, en la généralisant, l'équation d'Euler.
Le projet de refondation du Calcul des Variations était resté sans suite, mais Ampère avait procédé à une nouvelle rédaction du mémoire pour ses cours à l'École polytechnique. Publié en novembre 1825 dans les Annales de Gergonne, il en constitue la présentation la plus achevée.
Soit une équation V=F(x, y, p, q...) où entrent implicitement des paramètres a, b, c,...On observe en passant que, contrairement à Lagrange qui adopte pour les dérivées successives de y(x) la notation différentielle de Leibnitz, Ampère conserve les notations p, q, r,...d'Euler.
Comme y et ses dérivées successives sont fonction des paramètres a, b, c...
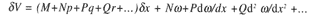
où M, N, P..sont les dérivées partielles de Vpar rapport aux x, y, p... et
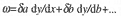
Le calcul de la variation de l'intégrale de Vdx conduit à l'intégrale :
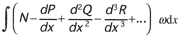
à laquelle s'ajoutent des termes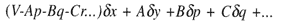 
qui, ironiquement, proviennent de l'intégration par parties des dérivées successives de 
.
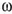Ampère néglige de faire figurer sous le signe somme les limites de l'intégrale mais indique que celle-ci, de même que les termes additionnels, doit être prise entre les limites données. Si celles-ci sont des points fixes où on se donne les x, y, p, q..., la réduction à zéro de la variation de l'intégrale V entraîne la nullité des termes additionnels et la condition d'extremum se réduit à :
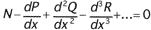
D'une discussion serrée des conditions aux limites résulte que cette condition d'extremum est satisfaite même si on ne se donne que les coordonnées des points fixes.
Suit l'examen des cas de dégénérescence, où l'ordre de l'équation d'extremum se réduit par suite de l'absence dans l'équation V de x ou de y.
L'étude détaillée de la chaînette, à laquelle Ampère nous convie ensuite, montre à l'évidence que sa méthode, pour générale qu'elle soit, apparaît beaucoup plus compliquée que celle de Lagrange.
Commencée avec la Géométrie, c'est avec elle que se termine l'œuvre mathématique d'Ampère. Le 14 septembre 1835 en effet, alors qu'il ne restait à Ampère que 9 mois à vivre, les Comptes rendus de l'Académie des sciences annoncent que « M. Ampère dépose sur le bureau une figure géométrique dans laquelle la construction très simple qu'il a trouvée pour diviser la circonférence de cercle en 17 parties égales est représentée ».Il s'agit en fait du troisième membre de la famille des polygones réguliers dont le nombre de côtés est égal à l'un des nombres de Fermat : Fn=2 exp 2n+l. Pour n=2, on obtient le polygone à 17 côtés, pour n=3, celui à 257 côtés etc.. On trouve, dans la septième et dernière partie des Disquisitiones Arithmeticae, la démonstration qu'ils existent et sont constructibles avec la règle et le compas. Cette démonstration, le génial Gauss l'avait donnée, dès 1796, à l'âge de 19 ans. Les brouillons de calculs retrouvés à l'Académie montrent qu'Ampère a essentiellement repris les calculs de Gauss dont il possédait les Disquisitiones.
Le sort a voulu que l'achat par Ampère de la maison de la rue des Fossés-Saint-Victor en 1819 constitue une sorte de retour aux sources. Cette demeure se trouvait en effet à deux pas du Jardin du Roi, à proximité duquel son intendant Monsieur de Buffon avait acquis en 1772 l'hôtel Lebrun. En ce siècle prodigue en Génies précoces celui qui, oublieux qu'à 16 ans il avait assimilé le calcul infinitésimal de Leibnitz, n'avait-il pas déclaré, alors qu'à 42 ans il n'était encore que Georges-Louis Leclerc : « Un homme doit considérer comme nulles les quinze premières années de sa vie ».
Se trouvent ainsi proches dans le souvenir l'enfant qui avait appris à lire dans l'Histoire des Oiseaux et l'auteur de l'Histoire Naturelle.
(*) Il est sans doute fait allusion à 4 pages autographes intitulées : Sur les probabilités, fait à Poleymieux où sont des choses curieuses. Autres morceaux sur les probabilités. Si la chronologie d'Ampère, souvent du domaine de l'hypothèse est exacte, les "choses curieuses" pourraient être la levée de l'hypothèque sur la maison de Poleymieux. On lit : "Problème Général. Déterminer la probabilité de deux joueurs, jouant ensemble à un jeu quelconque dans tous les cas qu'on peut proposer... " Trois règles du jeu sont ensuite définies dont la dernière, fondée sur un nombre non limité de parties, est : "La moins usitée mais la plus curieuse quant aux calculs". Suit une digression de 3 pages sur le fameux triangle qui avait permis à Pascal de résoudre, en 1653, le problème de la répartition des mises dans le cas d'arrêt d'un jeu avant sa conclusion.
