



Le 2 juin 1862 [1], Jean-Victor Poncelet présenta à ses collègues de l'Académie des sciences le premier tome des Applications d'analyse et de géométrie qu'il venait de faire paraître chez Mallet-Bachelier [2]. Il avait alors près de 74 ans et avait renoncé depuis longtemps à ses recherches de géométrie pour se consacrer entièrement à la mécanique appliquée. Le contenu de l'ouvrage avait été rédigé en fait bien des années auparavant. Il s'agissait de sept cahiers écrits entre mars 1813 et juin 1814, alors que Poncelet n'était qu'un obscur officier du génie prisonnier à Saratoff en Russie, et restés depuis à l'état manuscrit. Comme il l'écrivait lui-même dans la préface, il s'était "fait un devoir scrupuleux de n'y apporter, à l'impression, aucun perfectionnement qui eût pu en altérer le sens, en modifier les conséquences et les résultats algébriques, géométriques, etc." [3]. À la fin de la séance, Poncelet déposa aux archives de l'Académie, comme pièce justificative, le 7e et dernier cahier [4].
En publiant au soir de sa vie des papiers oubliés depuis près de cinquante ans, Poncelet entendait réparer une injustice. Ses contemporains n'auraient reconnu ni l'importance, ni l'antériorité de ses découvertes. Poncelet visait Chasles et Gergonne tout aussi bien que les analystes qui, à la suite de Cauchy, avaient contesté son principe de continuité. Poursuivant l'œuvre commencée avec l'aide de Mannheim et Moutard, il eut le temps, avant sa mort en 1867, de publier encore le deuxième tome de ses Applications d'analyse et de géométrie [5], et de rééditer en deux tomes son Traité des propriétés projectiles des figures, avec de très nombreuses additions [6]. Ces textes, le plus souvent inédits, révélaient la précocité de ses recherches. Poncelet atteignait ainsi le but qu'il s'était fixé : faire la preuve qu'il était le véritable créateur de la géométrie moderne. Mais il faisait mieux encore : avec la publication de son manuscrit de Saratoff, il entrait, à côté de ses contemporains Galois, Abel et Lobatchevski, dans la légende romantique des génies mathématiques solitaires et incompris. Quelle grandeur, en effet, chez ce jeune inconnu de 25 ans, inventant un nouveau chapitre des mathématiques dans "l'extrême isolement" d'un exil au milieu des steppes! Poncelet lui-même, tout en se défendant de comparer "ce livre modeste" avec le chef-d'œuvre de Chateaubriand, n'évoquait-il pas d'ailleurs comme titre possible, dans sa préface de 1862, les Mémoires d'outre-tombe ?
C'est que le manuscrit de Saratoff portait en germe toute l'œuvre ultérieure de Poncelet. Dans le 1er cahier, il étudiait les systèmes de cercles sur un plan et introduisait la notion de corde imaginaire. Le 2e cahier, rajouté semble-t-il après coup au recueil [7], contenait un exposé analytique de la théorie des coniques. Les quatre suivants exposaient la méthode des projections et formaient comme une première esquisse de ce qui allait devenir le Traité des propriétés projectives des figures [8] : les 3e et 4e cahiers traitaient des principes fondamentaux de la projection centrale et des polygones inscrits ou circonscrits à une conique, le 5e cahier, du système de deux coniques sur un plan, et le 6e, des polygones inscrits et circonscrits à deux coniques. Enfin, le 7e et dernier cahier contenait le début d'un mémoire reprenant la matière des cahiers précédents que Poncelet se proposait de présenter à l'Académie de Saint-Pétersbourg mais qu'il dut brusquement interrompre à la notification de la paix en juin 1814 [9].
Bien qu'il ait beaucoup fait pour la gloire posthume de Poncelet, le manuscrit de Saratoff n'a guère excité jusqu'à présent la curiosité des historiens. Il n'a fait l'objet d'aucune étude historique, pas plus d'ailleurs que les autres matériaux préparatoires au Traité des propriétés projectives des figures [10]. Cette lacune est d'autant plus regrettable que l'abondante documentation laissée par Poncelet permettrait de suivre étape par étape le développement de sa pensée, de déterminer précisément à chaque étape les influences qu'il a subies et de mettre ainsi en contexte une œuvre qui n'est en rien celle d'un génie isolé. Je voudrais ici beaucoup plus modestement esquisser une analyse de ses recherches initiales, antérieures à son retour en France à la fin de 1814, en me concentrant sur l'introduction des éléments imaginaires en géométrie et l'élaboration progressive de son principe de continuité [11]. On verra que loin d'être un point de départ, son travail à Saratoff s'inscrit dans un programme de recherche dont l'origine remonte à son séjour à l'École polytechnique, entre 1808 et 1810, et qui se rattache directement aux préoccupations d'autres mathématiciens de son temps, en particulier à celles de Brianchon. L'originalité de Poncelet, dans ce contexte, est moins d'avoir inventé que d'avoir systématisé et généralisé les méthodes de ce qu'on appellait alors l'École de Monge [12].
Poncelet a été admis à l'École polytechnique en novembre 1807. L'enseignement de la géométrie y était encore entièrement dominé par la figure de Monge, le fondateur de l'École. Il comprenait à la fois un cours de géométrie descriptive assuré par Jean-Nicolas Hachette, un fidèle disciple de Monge, avec l'aide du dessinateur Pierre-Simon Girard, et un cours d'analyse appliquée à la géométrie, assuré également par Hachette en première année et, en principe, par Monge en deuxième année. Mais Poncelet, tombé malade en mai 1808, ne put avoir Monge comme professeur : après un congé de plusieurs mois dans sa famille adoptive, à Saint-Avold [13], il redoubla sa première année et lorsqu'il passa en seconde année, en novembre 1809, Monge, dont la santé s'était dégradée, se fit remplacer par Hachette, puis par François Arago.
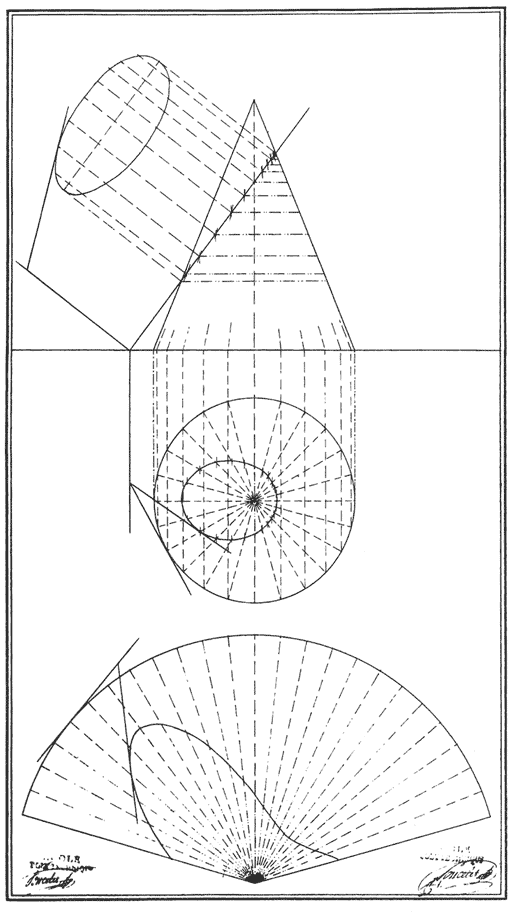
Bien qu'il ait donc seulement croisé Monge à l'École polytechnique sans pouvoir suivre son enseignement, Poncelet y subit profondemment son influence. Les exercices graphiques qu'il aimait pratiquer (fig. 1), l'étude assidue de ses grands traités et la fréquentation de ses disciples le mettait en contact avec la pensée du maître. Les épures de géométrie descriptive étaient pour lui une source de méditation [14]. Pendant son congé à Saint-Avold, en 1808, il commença à rédiger des "Notes de géométrie" [15] et en 1809, il présenta à Hachette les solutions de trois problèmes de géométrie élémentaire qui furent publiées dans la Correspondance sur l'Ecole polytechnique [16]. Il entrait ainsi dans le cercle des élèves de l'École qui consacraient leur loisir aux mathématiques avec le soutien et les encouragements des professeurs, selon une tradition inaugurée par Monge lui-même à Mézières. La plupart de ces élèves poursuivirent leurs recherches après leur sortie de Polytechnique, restant en contact avec leurs anciens maîtres et publiant dans la Correspondance d'Hachette, dans le Journal de l'École polytechnique et, après 1810, dans les Annales de mathématiques pures et appliquées fondées par Gergonne. Ils formèrent ce qu'on appellera après 1816 l'École de Monge [17]. Pour caractériser cette école mathématique, je retiendrai ici trois traits essentiels hérités de l'œuvre de Monge lui-même.
Le premier est le rôle primordial accordé à l'intuition géométrique. Monge dit-on [18], faisait de la géométrie avec les mains. Au contraire de la géométrie synthétique des Anciens, les démonstrations de "la géométrie générale et rationnelle" [19] que pratiquait l'École de Monge s'appliquent en effet à des représentations sans figures d'objets fictifs, généralement dans l'espace, comme des lignes, des plans et des surfaces illimités, disposés de façon arbitraire. Sa généralité était celle de l'imagination pure.
Mais le but de ces géomètres était loin d'être purement théorique. Ils recherchaient des constructions graphiques qui puissent éventuellement servir dans la pratique des arts, d'où un vif intérêt pour les méthodes de construction avec des instruments de précision, à la règle, au compas, à la règle et au compas, à l'équerre, etc. Leur principale source d'inspiration était la géométrie descriptive, qui ramène la construction des figures dans l'espace à des problèmes de construction graphique dans le plan. Elle permet d'ailleurs, inversement, de déduire de considérations de géométrie dans l'espace certaines propriétés des figures planes. Cette liaison réciproque, par la méthode des projections cylindriques, entre la géométrie plane et la géométrie dans l'espace, que Monge lui-même avait signalée dans son enseignement, frappa vivement ses disciples. Elle constitue pour Chasles la caractéristique principale de l'École de Monge [20].
Il existe cependant, pour caractériser cette école, un troisième trait fondamental : c'est le souci constant d'associer les méthodes analytiques aux méthodes géométriques, soit pour les comparer, soit pour les combiner. Dans son enseignement Monge ne cessait d'insister sur la correspondance existant entre les opérations de l'analyse et les constructions de la géométrie descriptive. Dans son œuvre mathématique, par exemple en théorie des courbes et des surfaces, il inventa et utilisa de manière systématique une méthode mixte analytico-géométrique à la fois intuitive et abstraite. Qu'ils choisissent plutôt l'approche géométrique ou l'approche analytique, les géomètres de l'École de Monge n'hésitaient pas à confronter l'une et l'autre et à évaluer leurs avantages respectifs sous le rapport de la généralité, de la facilité ou de l'évidence.
C'est dans ce contexte intellectuel que Poncelet entreprit ses recherches de géométrie, d'abord à l'École polytechnique, puis après plusieurs années d'interruption, en Russie. Le mémoire contenu dans le premier cahier de Saratoff offre à cet égard de précieuses indications [21]. Poncelet en commença la rédaction au plus tard en avril 1813, soit quelques semaines à peine après être arrivé à Saratoff au terme d'un voyage épuisant de plusieurs mois [22]. Comment croire qu'il se soit lancé dans cette entreprise sans avoir déjà à l'esprit une partie au moins de la matière qu'il allait traiter ? Mais comme Poncelet lui-même indique avoir délaissé les mathématiques après 1810 [23], l'origine du mémoire remonterait aux années passées à l'École polytechnique. C'est bien en effet, selon nous, ce que montre un examen attentif du texte.
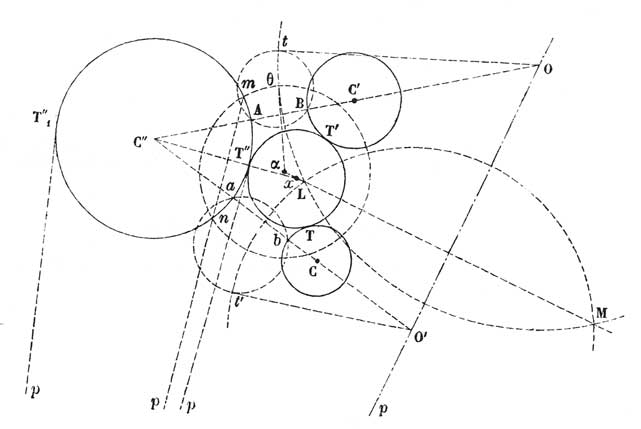

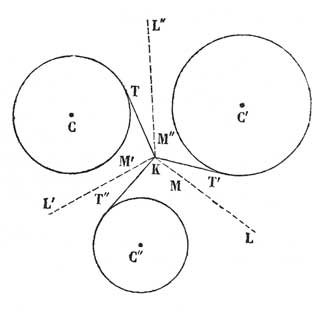
Notons d'abord que la première publication de Poncelet, en 1809, était consacrée, entre autres, à la construction à la règle et au compas d'un cercle tangent à trois cercles donnés [24] et que ce problème était étudié également dans le mémoire d'avril 1813, où Poncelet en proposait deux solutions [25]. La seconde était identique à celle de 1809. Quant à la première, elle utilisait les propriétés des cordes communes à un système de cercles (fig. 2). Notons C, C' C" les trois cercles, (x) le cercle tangent, T, T', T" ses points de contact avec C, C', C", et O, O', O" les centres de similitude directe de C' et C", C et C" et C et C'. Traitant d'abord le cas où le cercle (x) doit être soit extérieur soit intérieur aux trois cercles donnés, Poncelet montrait que le problème revient à construire un cercle tangent à C" tel que les tangentes à ce cercle menées de O et O' soient égales respectivement aux quantités T et T' avec
T2 = OT' x OT"
et T'2 = O'T x O'T".
Pour cette construction, Poncelet considérait la corde commune aux deux cercles auxiliaires de centres O et O' et de rayons T et T' et les deux points communs aux cercles orthogonaux à ces deux cercles, eux-mêmes situés sur l'axe de similitude direct 00' (points de base du faisceau des cercles conjugués aux deux cercles). Le cercle tangent est alors le cercle passant par ces deux points et tangent à C". On remarquera cependant sur la figure que les deux points de base ne peuvent être construits réellement si les deux cercles auxiliaires ont une corde commune réelle. Ce paradoxe posait le problème général de la construction d'une sécante commune à deux cercles indépendamment de la position relative de ces deux cercles. C'était là le point-clé du mémoire d'avril 1813.
L'idée de Poncelet consistait à définir la sécante commune à deux cercles comme le lieu des points d'où les tangentes aux cercles sont d'égale longueur (fig. 3) [26].
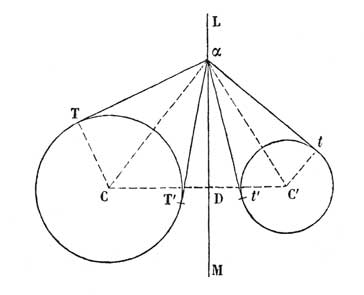
Cette définition, qui s'étend aussi bien à deux cercles (non concentriques) sans point commun, lui permettait de généraliser la notion de sécante commune et les propriétés qui lui sont liées, à n'importe quel couple de cercles (non concentriques) sur le plan [27]. Poncelet l'appliquait par exemple à la résolution du problème des cordes communes à trois cercles [28]. En projetant sur leur plan diamétral commun trois sphères qui se pénètrent mutuellement, Monge avait montré que les trois cordes communes à trois cercles qui se coupent deux à deux se rencontrent en un point (fig. 4) [29].
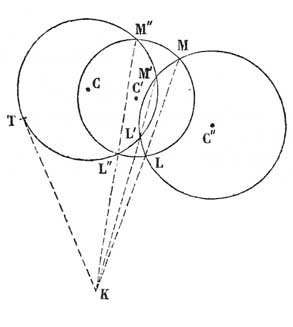  |

Par une démonstration directe, Poncelet généralisait facilement la proposition à trois cercles quelconques (ayant des centres distincts) grâce à sa définition générale d'une sécante commune à deux cercles. Il montrait également que les cercles orthogonaux à deux cercles donnés ont leurs centres sur la sécante commune aux deux cercles, et ont une corde commune sur la droite joignant les centres des deux cercles, ces sécantes ou cordes pouvant être réelles ou imaginaires [30]. C'est cette proposition qu'il utilisait dans sa construction du cercle tangent à trois cercles donnés.
La théorie exposée dans le mémoire d'avril 1813 équivalait en substance à la théorie des axes radicaux publiée par Gaultier de Tours dès 1812 dans le Journal de l'Ecole polytechnique [31]. Mais l'inspiration de Poncelet, qui ignorait alors le mémoire de Gaultier, était très différente [32]. Alors que Gaultier introduisait l'axe radical de deux cercles comme une construction sui generis, se confondant, quand les cercles se coupent, avec leur sécante commune, Poncelet partait de la notion ordinaire de corde commune à deux cercles, qualifiée de "réelle" et retendait au cas où, les deux cercles n'ayant aucun point commun, la corde est "imaginaire" [33]. Il s'agissait ainsi de dégager le point de vue constructif le plus général, indépendamment de la position respective des cercles sur le plan. L'objectif n'était donc pas d'inventer de nouvelles méthodes de construction, mais de généraliser les méthodes existantes applicables seulement jusqu'alors à des cas particuliers des figures.
Ce souci de généralité nous ramène une fois encore à l'École polytechnique [34]. Nous savons en effet par Poncelet lui-même que c'est au cours de sa scolarité à l'École qu'il commença à réfléchir sur les cas de possibilité et d'impossibilité dans la construction des figures [35]. L'une de ses sources d'inspiration se trouvait précisément, selon lui, dans "les élégants théorèmes de Monge sur les points, les droites et plans d'intersection des cercles et des sphères" que l'on retrouve dans son mémoire d'avril 1813. Une des méthodes favorites utilisées par Monge consistait à donner la démonstration géométrique d'une proposition pour une disposition particulière des figures, souvent en passant par la géométrie dans l'espace, et une démonstration analytique pour une disposition quelconque. Cette méthode offrait le double avantage de l'évidence par la synthèse et de la généralité par l'analyse. Monge se contentait d'ailleurs en général d'exposer la démonstration géométrique sur une disposition particulière des figures, en supposant tacitement la possibilité d'une généralisation par l'analyse. C'est ce que Chasles appellera plus tard la méthode des relations contingentes [36].
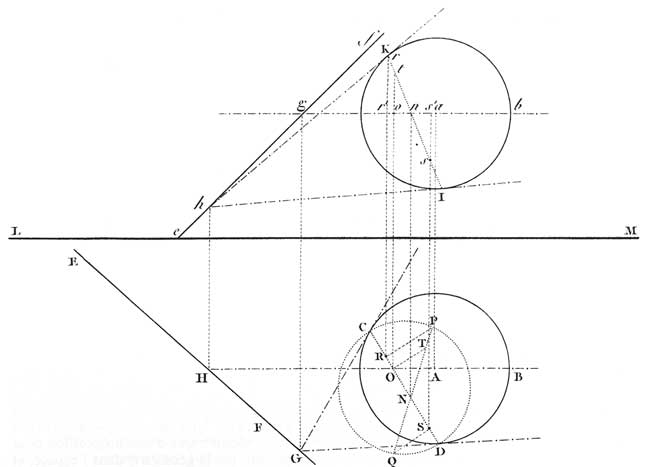
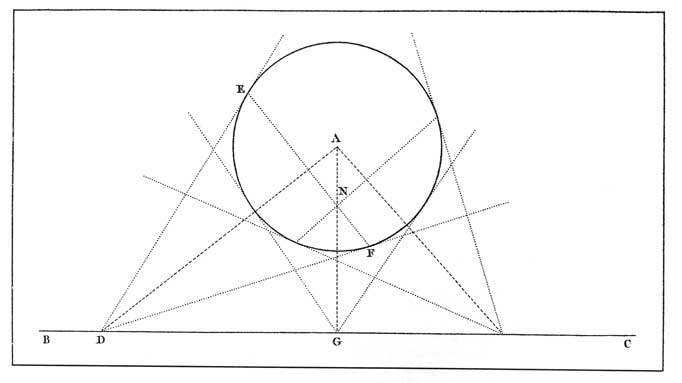
Monge en donnait dans sa Géométrie descriptive [37] un exemple classique (fig.5), analysé par Poncelet dans son manuscrit de Saratoff [38]. Lorsque le sommet d'un cône circonscrit à une sphère parcourt une droite donnée, le plan de son cercle de contact pivote autour d'un axe passant par les points de contact des deux plans tangents à la sphère menés par la droite. En considérant la trace des figures sur le plan diamétral de la sphère passant par la droite, Monge en déduisait que les cordes de contact des tangentes à un cercle menées par un point parcourant une droite passent toujours par un même point (qui est le pôle de la droite). Mais cette démonstration supposait que l'on puisse mener par la droite deux plans tangents à la sphère, c'est à dire, en se plaçant dans le plan diamétral, que la droite donnée ne coupe pas le cercle. Seule l'analyse permettait de généraliser ensuite le théorème à une disposition quelconque de la droite et du cercle.
Malgré son élégance, un tel mode d'exposition avait quelque chose d'insatisfaisant pour un esprit comme Poncelet. Ne pourrait-on plutôt donner aux démonstrations géométriques la même généralité qu'à l'analyse et éviter ainsi le recours à cette dernière ? C'est le but que Poncelet se fixa dès ses premières recherches. Dans son mémoire d'avril 1813, il donnait ainsi une démonstration du théorème sur le pôle d'une droite par rapport à un cercle pour une disposition quelconque de la droite en remarquant que ce pôle est le centre d'intersection (centre radical) des cordes réelles communes à trois cercles : le cercle donné et deux cercles quelconques centrés sur la droite et ayant leurs rayons égaux aux tangentes au cercle menés de leurs centres (fig. 6) [39].
C'est en voulant donner à la géométrie la même généralité qu'à l'analyse que Poncelet rencontra pendant ses études le problème de la continuité sur lequel il devait beaucoup méditer. Suivant sur ce point Lacroix, il considérait que les courbes étudiées dans le calcul suivent toujours la "loi de continuité", c'est à dire que leurs points successifs se succèdent sans aucun intervalle [40]. C'est cette propriété "métaphysique", c'est à dire non démontrable, qui expliquait selon lui que l'on puisse décrire les courbes par le mouvement d'un point générateur ou les surfaces par celui d'une ligne génératrice, et tracer une droite tangente ou un plan tangent en chacun de leurs points respectifs [41]. Analytiquement, cette propriété se traduit par la permanence des équations auxquelles satisfont les courbes et les surfaces, si bien que la loi de continuité y est admise tacitement et sans discussion. Géométriquement, en revanche, l'existence d'une loi de continuité est moins évidente. Le fait que la construction des points d'une courbe puisse dépendre de la disposition relative des figures qui servent à la définir semblait en effet introduire dans la question un élément fondamental de discontinuité.
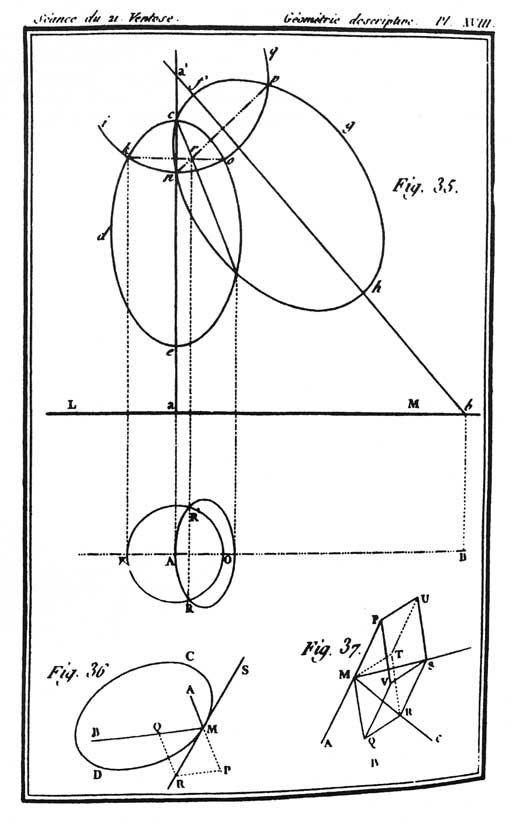
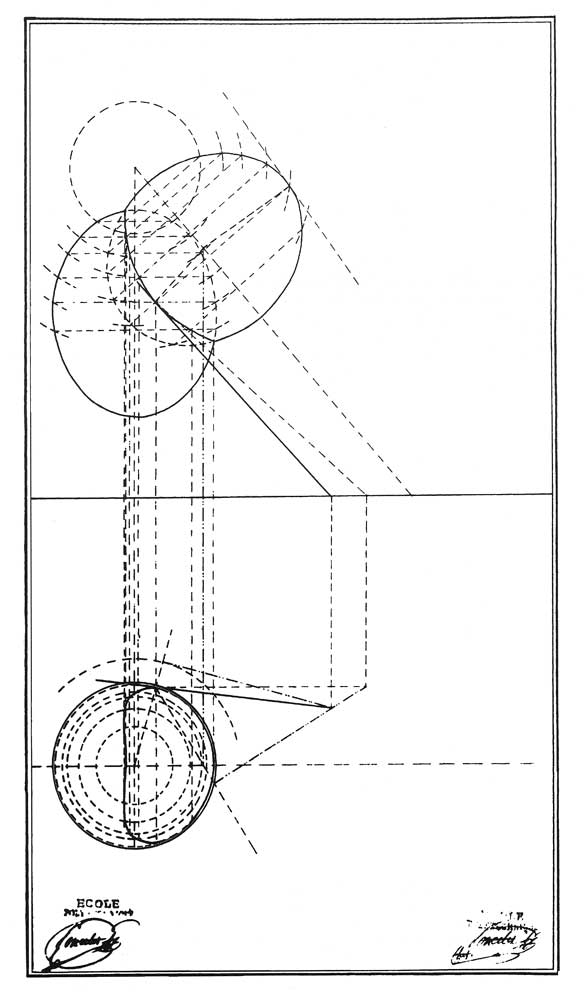
Poncelet paraît s'être d'abord posé le problème en étudiant à l'École polytechnique l'épure relative à l'intersection de deux ellipsoïdes de révolution d'axes coplanaires donnée par Monge dans sa Géométrie descriptive [42]. Pour construire point par point la courbe d'intersection, celui-ci utilisait une famille de sphères auxiliaires centrées sur le point de rencontre des deux axes. Les points communs aux deux cercles d'intersection de chaque sphère avec chacun des ellipsoïdes appartiennent évidemment à la courbe recherchée. Pour construire l'épure correspondante (fig. 7), Monge prenait comme plan vertical le plan des axes et comme plan horizontal un plan perpendiculaire à l'axe d'un des deux ellipsoïdes. Dans le plan vertical, il se ramenait alors à la construction suivante : on trace d'abord un cercle dont le centre est à l'intersection des deux axes, puis les deux cordes communes à ce cercle et aux ellipses contours apparents des ellipsoïdes sur le plan vertical. Le point d'intersection de ces deux cordes est la projection verticale de deux points de la courbe recherchée et leurs projections horizontales s'en déduisent immédiatement en traçant une ligne de rappel passant par ce point jusqu'à ses rencontres avec le cercle, projection sur le plan horizontal, de l'intersection de la sphère et de l'ellipsoïde d'axe vertical.
La courbe d'intersection des ellipsoïdes peut être ainsi construite point par point. Mais cette construction suppose évidemment que les deux cordes tracées dans le plan vertical ont un point commun situé dans le domaine du plan où les deux ellipses se recoupent. Elle s'interrompt dès que le point d'intersection sort de ce domaine, et, a fortiori, dès que l'une des cordes devient imaginaire. D'un autre côté, considérée analytiquement, la projection de la courbe dans le plan vertical, qui, selon Poncelet, serait en général une hyperbole [43], peut se prolonger "par continuité" bien au-delà des limites où les cercles auxiliaires cessent de rencontrer les deux ellipses. La solution de ce paradoxe réside dans la considération des cordes idéales communes à un cercle et à une ellipse dont Poncelet a introduit l'usage dans son Traité des propriétés projectives des figures. Sans aller encore aussi loin, il semble avoir été ainsi amené, lorsqu'il était élève à l'Ecole polytechnique, à étudier la théorie des cordes communes à un système de cercles et même à envisager son extension au cas où les cordes cesseraient d'être réelles.
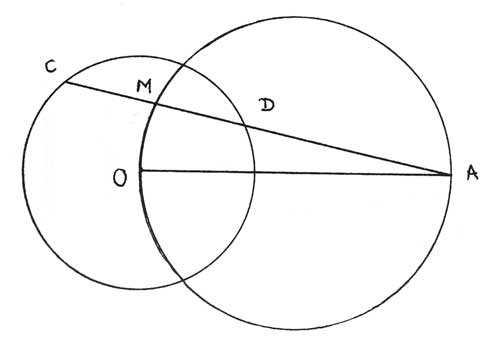
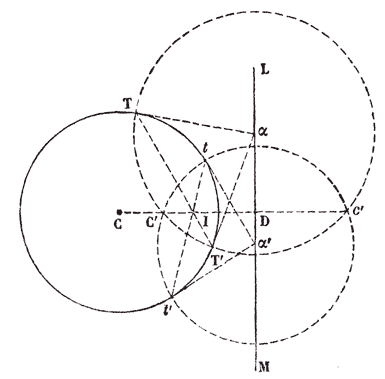
Un exemple simple, donné par Poncelet en 1862 [44], qui remonterait à l'époque de son séjour à l'École, illustre quel était alors l'état de ses réflexions. Considérons un cercle de centre O et une droite assujettie à passer par un point A (fig. 8). Si la droite est sécante réelle au cercle, on peut construire facilement point par point la courbe lieu des milieux des cordes interceptées : c'est un arc de cercle qui s'interrompt aux points de contact des tangentes menées du point A au cercle. Mais analytiquement, la courbe peut se prolonger en un cercle de diamètre AO. La "continuité" de la définition analytique s'oppose en apparence à la "discontinuité" de la construction géométrique. Mais Poncelet remarquait que pour construire géométriquement la courbe tout entière, il suffit de considérer le milieu de la corde interceptée comme le pied de la perpendiculaire à la droite menée du point O. La construction est alors toujours possible, que la droite soit sécante réelle au cercle ou pas.
Si cet exemple révèle le souci qu'avait Poncelet dès avant 1810 de donner aux méthodes géométriques la même généralité qu'aux méthodes analytiques, il semble indiquer qu'il cherchait alors à contourner la difficulté, comme le fera un peu plus tard Gaultier, en substituant à des constructions particulières des constructions applicables à tous les cas. Dans le mémoire d'avril 1813, en revanche, il affirmait la permanence d'une certaine disposition des figures, quand une droite rencontre un cercle, en l'étendant à des cas géométriquement impossibles. Mais sa définition d'une sécante imaginaire commune à deux cercles, bien que fondée sur une propriété générale de position, ressemblait à un procédé ad hoc dont l'origine demeurait énigmatique. Il restait à donner les principes justifiant l'introduction de tels éléments imaginaires en géométrie. C'est ce que Poncelet tentait de faire dans la suite du manuscrit de Saratoff, fondant ainsi ce qui allait devenir la géométrie projective.
En publiant en 1862 son mémoire d'avril 1813, Poncelet notait le caractère projectif des propriétés qui y étaient démontrées, mettant ainsi en évidence l'unité d'inspiration qui aurait animé son travail à Saratoff. Pourtant, il existe des différences frappantes entre ce premier mémoire et les cahiers suivants. Le mémoire d'avril 1813 était rédigé de manière impersonnelle et dans le style de la géométrie synthétique. Dans les cahiers suivants, en revanche, Poncelet combinait les méthodes analytiques et géométriques, accompagnant ses démonstrations de nombreuses réflexions personnelles sur les principes de la géométrie. D'autre part, le mémoire d'avril 1813, commencé alors que Poncelet venait d'arriver à Saratoff, reprenait, comme on l'a vu, l'étude initiée par Monge des systèmes de cercles, de leurs centres d'homothétie et de leurs cordes communes. Dans les cahiers suivants, dont la rédaction avait été précédée, semble-t-il, par une révision générale des éléments d'algèbre, d'analyse et de géométrie [45], Poncelet résolvait des problèmes sur les coniques et les polygones inscrits et circonscrits aux coniques que Brianchon avait remis à l'honneur quelques années auparavant. Finalement, alors que le mémoire d'avril 1813 était le point d'arrivée d'un travail probablement commencé dès son séjour à l'École polytechnique, les cahiers suivants constituaient le point de départ d'une œuvre de longue haleine qui devait aboutir au Traité des propriétés projectives des figures.
Comme Poncelet lui-même l'a expressément reconnu, l'origine de ses recherches sur les coniques se trouve dans l'œuvre de Charles-Julien Brianchon, un polytechnicien de la promotion 1803, devenu officier d'artillerie. Dans un mémoire publié dans le Journal de l'École polytechnique en 1806, Brianchon avait énoncé le fameux théorème qui porte son nom sur les hexagones circonscrits à une conique, dual du théorème de Pascal sur les hexagones inscrits dans une conique [46] et déduit de ces deux théorèmes la théorie des pôles et polaires pour les coniques et les quadriques. Ce premier mémoire, rédigé alors qu'il était encore élève à l'École polytechnique, avait été suivi par plusieurs notes dans la Correspondance sur l'École polytechnique. C'est ainsi qu'il y posait le problème, un parallélogramme, une droite et un point étant donnés dans un plan, de la construction à la règle seulement, d'une droite parallèle à la droite donnée, et passant par ce point. Problème dont Poncelet publia une solution lorsqu'il était élève à l'École [47]. Mais c'est principalement le second mémoire publié par Brianchon dans le Journal de l'École polytechnique en 1810 qui inspira Poncelet à Saratoff [48].
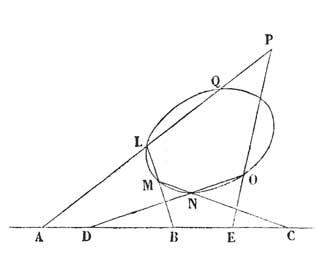
Dans ce mémoire, rarement mentionné par les historiens de la géométrie, Brianchon appliquait la méthode de projection centrale à la résolution de problèmes de géométrie "qui se rapportent seulement aux directions des lignes et dans lesquelles on ne considère aucunement les longueurs absolues ou relatives de ces lignes, non plus que la grandeur des angles" [49]. Il y démontrait en particulier le théorème suivant, donné par MacLaurin : supposons qu'un polygone dont tous les sommets sauf un sont situés sur une conique se déforme sans que ses côtés cessent de passer chacun par un point fixe ou pôle (fig. 9) ; alors, si ces pôles sont alignés, le sommet libre décrira une conique. Ce théorème se déduisait facilement de la mise en équation du problème, une fois la droite des pôles envoyée à l'infini [50]. En l'appliquant à diverses configurations, Brianchon obtenait une solution élégante pour de nombreux problèmes classiques de géométrie, tels que la construction d'un cercle passant par deux points donnés et tangent à un cercle donné, ou celle de la tangente à une conique passant par un point donné, ou encore celle des points où une droite donnée rencontre une conique donnée seulement par ses axes. Il en déduisait également le célèbre théorème de MacLaurin, selon lequel le troisième sommet d'un triangle mobile dont les deux premiers sommets parcourent deux droites données et dont les côtés passent chacun par un point fixe, décrit une conique, équivalent lui-même au théorème de Pascal sur les hexagones inscrits à une conique. Enfin Brianchon énonçait le théorème suivant, qui illustre la théorie des polaires réciproques : lorque la sécante à une conique enveloppe une deuxième conique, son pôle décrit une troisième conique (fig. 10). Pour le démontrer, il se ramenait par une projection centrale au cas simple où les deux coniques données sont des cercles.

Partant de cet important mémoire, dont il avait fait de toute évidence une lecture très attentive à l'époque de sa publication, Poncelet entreprit donc pendant son séjour de Saratoff de développer systématiquement la méthode de la projection centrale, méthode consistant, notait-il au début de son 3e cahier en citant Brianchon et Carnot, "à employer la géométrie pour ramener la question proposée à une autre beaucoup plus simple, et qui, bien qu'elle en soit un cas particulier, la comprend néanmoins en vertu de l'extension qu'elle peut recevoir au moyen d'une proposition ou d'une construction géométrique auxiliaire" [51].
Je ne chercherai pas ici à donner une analyse complète et systématique de ce travail, ni à rendre compte de tous les résultats obtenus [52], et je me limiterai aux principes sur lesquels ils sont fondés. Dans ses premières recherches exposées dans le 3e cahier, Poncelet énonçait cinq principes fondamentaux et élémentaires de la projection centrale. Les trois premiers, donnés sans démonstration, affirment l'équivalence projective d'un cercle et d'une conique d'une part, d'un faisceau de droites parallèles et d'un faisceau de droites sécantes de l'autre. Les deux derniers, beaucoup plus délicats à établir, affirment d'une part l'équivalence projective d'un système d'une conique et d'une droite à distance finie et du système d'un cercle et d'une droite à l'infini (4e principe) [53], de l'autre l'équivalence du système de deux coniques et du système de deux cercles (5e principe) [54]. Comme on l'a vu, c'est sur ces deux principes que Brianchon s'apppuyait dans son mémoire de 1810.
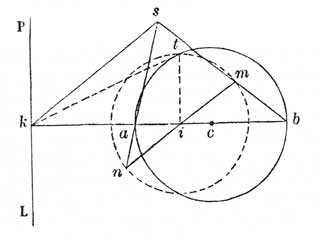
Poncelet donnait une démonstration du 4e principe par la géométrie descriptive [55]. On se ramène d'abord au cas où la conique est un cercle au moyen du 1er principe. Le problème revient alors à déterminer le sommet s d'un cône ayant pour base le cercle donné C et tel que toute section parallèle au plan passant par s et par la droite donnée PL soit un cercle, dit sous-contraire à C. En effet, la projection de centre s du plan de base sur l'un des plans de section ainsi déterminés transforme C en un autre cercle et envoie PL à l'infini. Dans l'épure tracée par Poncelet (fig. 11), le plan horizontal est le plan de base du cône et contient PL, et le plan vertical passe par le centre c de C, et est perpendiculaire à PL ; Poncelet montrait qu'il suffit pour résoudre le problème de mener du point k où la ligne de terre rencontre la droite donnée l'une des deux tangentes à C, puis, t étant le point de contact de la tangente avec C, de tracer dans le plan vertical le cercle de centre k et de rayon r - kt. Tous les points du cercle ainsi construits, à l'exception des deux points situés dans le plan horizontal, peuvent être pris comme sommet s du cône recherché, les plans de projection étant alors les plans parallèle au plan de bout passant par k et s. Poncelet montrait en outre que les centres des cercles sous-contraires de C sont les points d'une droite du plan vertical passant par s et rencontrant la ligne de terre en i, pôle de la droite donnée par rapport à C. On a donc toujours la relation kc.ki = kb.ka, où c est le centre de C et a et b sont les points d'intersection de C avec la ligne de terre.
Cette construction exige que la droite PL ne rencontre pas le cercle C, sinon il n'est plus possible de mener de k les tangentes au cercle. Poncelet obtenait donc une démonstration géométrique de son 4e principe pour une disposition particulière des figures. Il la considérait néanmoins comme une démonstration générale. Il notait d'abord que, dans le cas même où, PL rencontrant C, les cercles sous-contraires ont cessé d'exister réellement, le point i lui-même demeure constructible en tant que pôle de PL. Dans le langage du Traité des propriétés projectives, i est devenu le centre idéal d'un cercle dont le rayon est imaginaire. Poncelet faisait ensuite appel à "un principe tacitement admis par beaucoup de géomètres, mais non jusqu'ici démontré ou explicitement démontré" [56]. Ce principe, qu'il devait énoncer un peu plus tard en ouverture de son mémoire pour l'Académie de Saint-Pétersbourg (7e cahier de Saratoff), dit "que si une figure quelconque jouit d'une de ces propriétés que nous appelons de position, quand les parties dont elle se compose ont une disposition particulière, cette figure jouit encore de la même propriété quelle que soit la manière générale dont on ait interverti l'ordre ou la disposition respective des figures" [57].
Même si ce principe était déjà implicitement utilisé par Monge, comme il le remarquait un peu plus loin, Poncelet lui donnait une plus grande extension. Il introduisait en effet directement dans les raisonnements de géométrie des éléments imaginaires qui ne peuvent "se peindre à l'imagination par des objets sensibles", ce que n'avait jamais fait Monge. Poncelet lui-même, dans son mémoire d'avril 1813, avait considéré comme on l'a vu des "cordes imaginaires", mais il s'agissait encore d'éléments constructibles, ce qu'il appellera plus tard des éléments idéaux. En revanche le cercle sous-contraire à C de centre i et ses tangentes sont inconstructibles quand PL rencontre C.
Pour justifier l'introduction de pareils éléments en géométrie, Poncelet s'appuyait sur l'analyse. On trouve en effet dans le mémoire pour l'Académie de Saint-Pétersbourg une solution analytique du problème, montrant que le rayon du cercle sous-contraire à C de centre i est réel quand la corde de C intercepté par PL est imaginaire et imaginaire quand la corde est réelle [58]. Dans le 3e cahier, en revanche, Poncelet considérait la question de plus haut. Quand on met en équation un problème de géométrie, remarquait-il, on part d'une disposition particulière des figures, mais les résultats qu'on obtient sont vrais pour toutes les dispositions possibles car les formules finales ne gardent pas trace de la disposition primitive. C'est ce qui donne aux méthodes analytiques leur grande généralité. Or, personne n'a jamais réussi à justifier de manière rigoureuse cette "puissance de l'analyse". "On y croit, mais cela suffit-il?", se demandait finalement Poncelet. Question rhétorique, à laquelle il ne cherchait pas de réponse. Mais en la soulevant, il posait le dilemme fondamental : si l'on refuse en géométrie d'étendre les résultats des cas possibles aux cas impossibles, il faut y renoncer également en analyse, dont la généralité n'est pas mieux démontrée. Poncelet a reproduit ces réflexions après l'énoncé du principe dans son mémoire pour l'Académie de Saint-Pétersbourg [59].
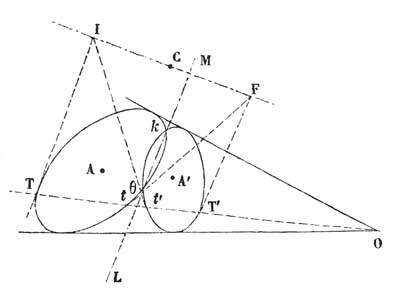
L'étude du 5e principe, que Brianchon avait énoncé sans démonstration dans son mémoire de 1810, donnait à Poncelet une nouvelle occasion d'appliquer sa théorie des éléments imaginaires en géométrie. Selon ce principe, deux coniques peuvent être transformées par projection en deux cercles. Poncelet en proposait deux démonstrations analytiques, la première utilisant le 4e principe [60], la seconde entièrement indépendante mais beaucoup plus laborieuse [61]. Il montrait ainsi que, géométriquement parlant, le centre de projection doit être sur un cercle vertical centré sur le milieu C d'une des cordes communes aux deux coniques et que le rayon de ce cercle peut être réel ou imaginaire selon que la corde elle-même est imaginaire (IF) ou réelle (ML) (fig. 12). Il en résulte en particulier que le système de deux coniques ayant quatre points communs ne peut se projeter selon un système de deux cercles. Le point qui nous intéresse ici concerne l'existence géométrique des cordes "imaginaires" correspondant aux centres de projection constructibles.
C'est d'abord, semble-t-il, en étudiant dans le 4e cahier le problème de l'inscription dans une conique d'un polygone ayant un nombre pair de côtés passant par des pôles alignés que Poncelet mit en évidence le fait que deux coniques sans points communs réels peuvent néanmoins avoir des points communs imaginaires [62]. Dans le cas étudié où les points communs sont des points de contact, il montrait qu'analytiquement la condition de contact entre les deux coniques a toujours lieu mais que les points de contact eux-mêmes peuvent devenir imaginaires et qu'alors "le contact n'existe plus physiquement ou graphiquement" et il en concluait que "deux coniques qui ne se coupent pas peuvent néanmoins être liées entre elles, géométriquement ou par certaines relations graphiques, de la même manière que si elles se coupaient ou se touchaient effectivement, et elles peuvent, dans l'un et l'autre cas, posséder les mêmes propriétés relatives" [63]. Cette remarque restait cependant assez vague. À l'époque de sa rédaction, il semble bien qu'il manquait encore à Poncelet une véritable théorie des tangentes et cordes communes à deux coniques.
Cette théorie est esquissée seulement dans le 5e cahier [64]. Poncelet y montrait que deux coniques ayant une corde réelle commune ont également une corde "fictive" mais constructible conjuguée à la première, qu'il baptisait alors "droite magistrale" et que deux coniques extérieures l'une à l'autre et sans aucun point commun ont deux cordes "fictives" mais constructibles. Toute cette étude reposait elle-même sur l'application du 5e principe au système de deux cercles étudié dans le mémoire d'avril 1813, la droite magistrale n'étant que la transformée de leur sécante imaginaire commune à l'infini. On notera que l'interprétation géométrique de la démonstration analytique du 5e principe que donnait Poncelet reposait donc sur des résultats déduits eux-mêmes de ce principe ! Une telle maladresse, sans être une faute logique, révèle les difficultés que Poncelet rencontrait alors pour justifier géométriquement le 5e principe. Il évitait d'ailleurs de discuter le cas délicat où l'une des coniques étant entièrement intérieure à l'autre, leurs cordes communes deviennent tout à fait impossibles à construire.
Deux voies s'ouvraient alors à Poncelet pour éclairer la question au point de vue de la géométrie synthétique. La première consistait à développer une théorie des cordes communes à deux coniques indépendante du 5e principe. Dès cette époque, il élabora, semble-t-il, sa théorie des cordes idéales qu'il comptait exposer dans son mémoire pour l'Académie de Saint-Pétersbourg [65], mais il n'en eut pas le temps. On retrouve cette théorie dans l'Essai sur les propriétés projectives des figures, rédigé en 1818, puis dans le Traité des propriétés projectives des figures, où elle joue, comme on sait, un rôle fondamental. La seconde voie consistait à préciser la signification du principe métaphysique d'extension des cas possibles aux cas impossibles. À quelles propriétés des figures ce principe peut-il légitimement s'appliquer ?
Dans son mémoire pour l'Académie de Saint-Pétersbourg, Poncelet distinguait, en partant de l'analyse, deux espèces de propositions de position, celles qui ne tiennent à aucune grandeur déterminée ou qui ne tiennent qu'à des grandeurs ne pouvant jamais devenir imaginaires, dont la vérité géométrique est absolue, et celles qui tiennent à des grandeurs pouvant devenir imaginaires, dont la vérité géométrique est conditionnelle [66]. Les 4e et le 5e principes entrant eux-mêmes dans la catégorie des propositions dont la vérité géométrique est conditionnelle, il semblerait que la vérité des propositions qui s'en déduisent est elle aussi conditionnelle. Mais Poncelet maintenait par ailleurs que, "quoique la projection d'une figure donnée puisse devenir imaginaire pour certaines dispositions de cette figure, il n'en est pas moins vrai de dire que toute propriété dont jouit sa projection quand elle est possible, est toujours une propriété de cette figure, même quand la projection devient imaginaire" (c'est Poncelet qui souligne) [67]. C'est pour échapper à de telles inconsistances que Poncelet inventa son principe de continuité en 1815-1816, après avoir lu de manière approfondie la Géométrie de position de Carnot [68].
1 Comptes rendus des séances de l'Académie des sciences, tome 54, 2 juin 1862, pp. 1144-1148.
2 J.-V. Poncelet, Applications d'analyse et de géométrie qui ont servi, en 1822, de principal fondement au Traité des propriétés projectives des figures, etc., tome 1er, Paris, Mallet-Bachelier, 1862 (AAG, 1).
3 AAG, 1, Préface, p. xij.
4 Ce cahier est aujourd'hui conservé à la bibliothèque de l'Institut de France sous la cote ms 2381, recueil VI.
5 J.-V. Poncelet, Applications d'analyse et de géométrie qui ont servi, en 1822, de principal fondement au Traité des propriétés projectives des figures, etc., tome 2, Paris, Gauthier-Villars, 1864 (AAG, 2). Ce tome contient les sept cahiers manuscrits inédits rédigés par Poncelet entre son retour de Russie, en 1814, et la publication de son Traité des propriétés projectives des figures en 1822. On y trouve en particulier le texte de son "Essai sur les propriétés projectives des sections coniques" présenté à l'Académie des sciences le 1er mai 1820.
6 J. V. Poncelet, Traité des propriétés projectives des figures, ouvrage utile à ceux qui s'occupent des applications de la géométrie descriptive et d'opérations géométriques sur le terrain, deuxième édition, revue, corrigée et augmentée d'annotations nouvelles, Paris, Gauthier-Villars, tome 1er, 1865, et tome 2, 1866 (TPP, 1 et 2). Le tome 1er contient le texte même du Traité de 1822. Le tome 2 contient les mémoires présentés à l'Académie des sciences dans les années suivantes ("Théorie générale des centres de moyennes harmoniques" et "Théorie générale des polaires réciproques" en 1824, "Analyse des transversales appliquée aux courbes et surfaces géométriques" en 1831) ainsi qu'un mémoire sur les systèmes de lignes et de surfaces géométriques d'ordre quelconque achevé en 1831 mais jamais présenté et des extraits de sa polémique avec Gergonne sur la dualité. De nombreuses notes rédigées pour cette édition complètent les textes originaux.
7 Une note de Poncelet jointe au manuscrit conservé à la bibliothèque de l'Institut de France indique l'existence de six cahiers seulement. Le dernier cahier est lui-même numéroté comme le 6e. Il semble que Poncelet a rajouté le 2e cahier, entièrement consacré à la géométrie analytique, pour indiquer quel était alors le développement de ses idées (voir AAG, 1, pp. 56-57, note) et aussi pour alléger les développements analytiques du 5e cahier (voir AAG, 1, p. 263, note).
8 Voir à ce propos la préface du Traité des propriétés projectives des figures écrite par Poncelet en 1822.
9 D'après le manuscrit conservé à la bibliothèque de l'Institut de France, ce mémoire aurait pu s'intituler "Sur une classe de propriétés intéressantes connues et inconnues" ou "Mémoire sur une classe intéressante de propriétés géométriques des figures".
10 Les analyses de l'œuvre de Poncelet remontent pour la plupart au XIXe siècle et au début du XXe siècle et s'inscrivent dans des exposés généraux sur l'histoire de la géométrie projective. Citons en particulier M. Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométris, 1837 et E. Kôtter, Die Entwicklung der synthetischen Géométrie von Monge bis auf Staudt (1847), Leipzig, 1901. Parmi les travaux plus récents, on pourra se référer à J. L. Coolidge, A History of geometrical methods, Oxford, 1940 et à D. Lehmann et R. Bkouche, Initiation à la géométrie, Paris, PUF, 1988, appendice historique.
11 Je remercie Karine Chemla et Joël Sakarovitch pour leurs observations critiques qui ont aidé à améliorer ce texte.
12 C'est le point de vue défendue par R. Taton, L'Œuvre scientifique de Monge, Paris, 1951, pp. 273-276.
13 I. Didion, "Notice sur la vie et les ouvrages du général J.-V. Poncelet", Mémoires de l'Académie de Metz, tome 50, 1870, pp. 101-159.
14 Voir AAG, 1, pp. 447-461, où Poncelet a publié des recherches entreprises en 1809 sur le tracé des tangentes aux courbes de contour apparent et de séparation d'ombre et de lumière dans l'épure de la vis à filets triangulaires.
15 I. Didion, art. cit..
16 Correspondance sur l'École polytechnique, tome 2, pp. 271-274.
17 Voir Ch. Dupin, Essai historique sur les services et les travaux scientifiques de Gaspard Monge, Paris, 1819, p. 196, M. Chasles, op. cit., p. 191, et l'introduction du Traité des propriétés projectives des figures de J.-V. Poncelet.
18 M. Chasles, op. cit. p. 209.
19 L'expression se trouve sous la plume de J.-V. Poncelet et de M. Chasles.
20 Ibid., p. 191.
21 Le manuscrit de ce cahier est conservé dans les Archives de l'École polytechnique, titre IX, fonds Poncelet carton n°5. Le titre original du mémoire est "Notes sur la géométrie. Contacts des cercles et des lignes droites". Il est publié en 1862 sous le titre : "Lemmes de géométrie synthétique : sur les systèmes de cercles situés dans un même plan".
22 Dans la version imprimée du mémoire, Poncelet date le début de sa rédaction d'avril 1813. Le manuscrit indique fin mars, biffé.
23 AAG, 1, préface, p. ix. Poncelet est très discret sur son séjour à l'École d'application de l'artillerie et du génie de Metz où il a eu Français et peut-être Servois comme professeurs.
24 Correspondance sur l'École polytechnique, tome 2, pp. 271-273.
25 AAG, 1, pp. 30-41, problème II
26 AAG, 1, pp. 12-16, proposition VI.
27 AAG, 1, pp. 15-16, proposition VI, scholie 1.
28 AAG, 1, pp. 17-19, proposition VIII.
29 Monge n'a jamais publié cette démonstration, que l'on trouve en revanche dans la Géométrie de position de Carnot (n° 305, pp. 347-348). Ce sont Poncelet (AAG, 1, p. 17) et Chasles {pp. cit., p. 207) qui lui en attribuent la paternité.
30 AAG, 1, pp. 21-23, proposition XI.
31 L. Gaultier, "Mémoire sur les moyens généraux de construire graphiquement un cercle déterminé par trois conditions et une sphère déterminée par quatre conditions", Journal de l'École polytechnique, 16e cahier, mai 1813, pp. 124-214.
32 Préface à la première édition du Traité des propriétés projectives des figures.
33 Les notions de "corde réelle" et de "corde imaginaire" sont introduites par Poncelet dans la démonstration de la proposition XI, AAG, 1, p. 22.
34 Sur le thème de la généralité au début du XIXe siècle, voir K. Chemla, "Lazare Carnot et la généralité en géométrie", Revue d'histoire des mathématiques, 1998, à paraître. Poncelet avait certainement pris connaissance de la Géométrie de position de Carnot pendant son séjour à l'École polytechnique mais il ne paraît l'avoir médité qu'après son retour en France à la fin de 1814 (voir AAG, 2, p. 547).
35 AAG, 1, pp. 427-428, note rédigée en 1862.
36 M. Chasles, Aperçu historique .... pp. 198-199 .
37 G. Monge, Géométrie descriptive, n° 39.
38 AAG, 1, pp. 125-126 et pp. 375-377.
39 AAG, 1, pp. 20-21, proposition X.
40 Voir S.F. Lacroix, Traité élémentaire de calcul différentiel et intégral, Paris, 1802, n°60, pp. 75-76. Poncelet a exprimé sa dette envers Lacroix et Poinsot in AAG, 2, p. 564.
41 Voir par exemple Poncelet, AAG, 2, pp. 581-592.
42 AAG, 1, pp. 426-427, note, AAG, 2, pp. 379-381 et TPP, 1, pp. 33-35.
43 Ce n'est pas toujours vrai, comme l'a montré La Gournerie. Voir TPP, 1, pp. 410-411.
44 AAG, 1, p. 427, note. Voir aussi AAG, 2, p. 580.
45 Voir AAG, 1, préface, pp. ix-x, et note, pp. 97-98.
46 CJ. Brianchon, "Sur les surfaces courbes du deuxième degré", Journal de l'École polytechnique, tome 6, 13e cahier, 1806, pp. 297-311. Le théorème de Pascal, dit parfois de ;'hexagrammum mysticum, énonce que les trois points de concours des côtés opposés d'un hexagone inscrit à une conique sont alignés ; le théorème de Brianchon énonce quant à lui que les trois diagonales joignant les sommets opposés d'un hexagone circonscrit à une conique se croisent en un même point.
47 Correspondance sur l'École polytechnique, tome 2, pp. 273-274 ; voir aussi AAG, 1, p. 446 et 77V, 1, pD. 102-103.
48 C. J. Brianchon, "Solution de quelques problèmes de géométrie", Journal de l'École polytechnique, tome 4, 10e cahier, novembre 1810, pp. 1-15. Poncelet reconnaît sa dette dans le Traité des propriétés projectives des figures (TPP, 1, introduction, p. xxiii) : "Je me fais un plaisir et un devoir de reconnaître que je dois l'idée première de mon travail à la lecture de cet écrit".
49 Ibid., p. 1.
50 Voir aussi AAG, 1, pp. 140-143.
51 AAG, 1, p. 116.
52 On y trouve en particulier, démontré par l'analyse et la géométrie, son beau théorème sur les polygones à la fois inscrits et circonscrits à deux coniques. D'après ce théorème, si l'on peut tracer un polygone à n côtés inscrit à une conique donnée et circonscrit à une autre conique donnée, on peut en tracer une infinité.
53 AAG, 1, p. 122. Dans le mémoire pour l'Académie de Saint-Pétersbourg (7e cahier), le 4e principe devient le 5e principe (AAG, 1, pp. 387-388) ; Poncelet donne en effet comme 4e principe l'équivalence projective du système d'un cercle et d'une droite à distance finie et de celui d'un cercle et d'une droite à l'infini (AAG, 1, p. 381).
54 Le passage du 3e cahier concernant le 5e principe n'a pas été publié (AAG, 1, pp. 262-263, note). Poncelet y donnait une démonstration qu'il jugea ensuite insuffisante. L'énoncé et les démonstrations du 5e principe se trouvent en fait dans le 5e cahier (AAG, 1, pp. 287-307). Dans le mémoire pour l'Académie de Saint-Pétersbourg (7e cahier), le 5e principe devient le 6e principe (AAG, 1, p. 408).
55 AAG, 1, pp. 118-123 et pp. 381-387.
56 AAG, 1, p. 124.
57 Ibid.,p. 374.
58 Ibid., pp. 388-408.
59 Ibid., pp. 374-375.
60 Ibid., pp. 288-290 et pp. 408-411.
61 Ibid., pp. 292-302 et pp. 411-420.
62 Ibid., p. 199.
63 Ibid., p. 200.
64 Ibid., pp. 262-287.
65 Ibid., p. 411. Poncelet indique qu'il a appelé "dans des notes de géométrie" du nom de cordes, de sécantes idéales, des cordes communes à deux coniques qui ne rencontrent ni l'une ni l'autre de ces courbes mais qui ne cessent pas d'exister, "les distinguant ainsi de celles qui sont entièrement illusoires et impossibles à construire, même en direction".
66 Ibid., p. 425.
67 Ibid., p. 378-379.
68 Dans son Traité des propriétés projectives des figures, Poncelet commente longuement son principe de continuité (voir en particulier TTP, 1, introduction, pp. XIII-XVI, et pp. 65-67) mais n'en donne pas d'énoncé. Il ressort du texte qu'il entendait par principe de continuité le principe selon lequel des propriétés descriptives ou métriques d'une figure considérée dans un état particulier sont conservées en général lorsque l'on fait varier la figure primitive par degrés insensibles ou selon un mouvement continu. L'interprétation du principe dépend de ce que l'on entend par les expressions vagues "propriétés descriptives ou métriques", "état particulier" et "état général" d'une figure.